CHAPTER 1: ALGEBRA
1.1 ORDERED PAIR
Definition: An ordered pair is a pair of numbers written in a specific order as (x, y), where: • x is called the first element • y is called the second element
Important Points: • (x, y) ≠ (y, x) unless x = y • Ordered pairs are used to represent points in coordinate geometry
Example: (2, 3) represents x = 2 and y = 3
Uses: • To represent relations • To locate points on a graph.
1.2 CARTESIAN PRODUCT OF TWO SETS
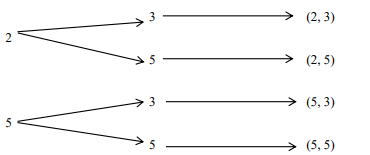
Definition: If A and B are two sets, then the Cartesian product of A and B is the set of all ordered pairs (a, b) such that: • a ∈ A • b ∈ B
Symbol: A × B
Example: If A = {1, 2} and B = {3, 4} Then, A × B = {(1,3), (1,4), (2,3), (2,4)}
Important Note: • A × B ≠ B × A
Figure:
1.3 RELATION
Definition: A relation is any subset of a Cartesian product of two sets.
If R ⊆ A × B, then R is a relation from A to B.
Types of Representation: • Roster form • Arrow diagram • Graphical representation
Example: A = {1,2,3} B = {2,4,6} Relation R = {(1,2), (2,4), (3,6)}
1.4 TYPES OF RELATIONS
(i) Reflexive Relation A relation R on a set A is reflexive if: (a, a) ∈ R for every a ∈ A
(ii) Symmetric Relation R is symmetric if: If (a, b) ∈ R, then (b, a) ∈ R
(iii) Transitive Relation R is transitive if: If (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R
Examples of each type are compulsory for exams.
1.5 FUNCTION
Definition: A function is a special type of relation where: • Each element of the domain has exactly ONE image in the codomain
Domain: Set of all first elements
Codomain: Set of all possible outputs
Range: Set of actual outputs
Important Condition: One‑to‑many relation is NOT a function
1.6 TYPES OF FUNCTIONS
(i) One‑One Function (Injective) Different inputs give different outputs
(ii) Many‑One Function Different inputs may give same output
(iii) Onto Function (Surjective) Every element of codomain has an image
(iv) Into Function Some elements of codomain have no image
(v) One‑One and Onto (Bijective) Both injective and surjective

ADDITIONAL EXAMPLES, SHORT TRICKS
ORDERED PAIR – EXAM EXAMPLES & TRICKS
Example: If (x, y) = (3, 7), then x = 3 and y = 7
If (x − 2, y + 3) = (4, 9) Then, x − 2 = 4 ⇒ x = 6 y + 3 = 9 ⇒ y = 6
SHORT TRICK: Whenever two ordered pairs are equal, ALWAYS equate first with first and second with second.
CARTESIAN PRODUCT – EXAMPLES & TRICKS
Example: If A = {a, b} and B = {1, 2, 3} Then, A × B = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3)}
Cardinality Trick: n(A × B) = n(A) × n(B)
IMPORTANT EXAM POINT: A × B ≠ B × A (unless A = B)
RELATION – EXAMPLES & QUICK METHODS
Example: A = {1,2,3}, B = {1,4,9} Relation R: "is square root of" R = {(1,1), (2,4), (3,9)}
EXAM TIP: Relation is ALWAYS a subset of A × B
DOMAIN & RANGE – FAST SOLVING
Rule: Domain = all first elements Range = all second elements
Example: R = {(2,3), (3,4), (3,5)} Domain = {2,3} Range = {3,4,5}
SHORT TRICK: Never repeat elements in domain or range
TYPES OF RELATION – EXAM SHORTCUT
Reflexive: (a,a) must exist for ALL a
Symmetric: If (a,b) exists, (b,a) must exist
Transitive: If (a,b) and (b,c) exist ⇒ (a,c) must exist
Equivalence: Reflexive + Symmetric + Transitive
FUNCTION – EXAMPLES & COMMON MISTAKES
Example: f = {(1,2), (2,4), (3,6)} ⇒ FUNCTION
NOT a Function: {(1,2), (1,3)} (same input, two outputs)
Golden Rule: ONE input → ONE output
VERTICAL LINE TEST – QUICK TRICK
Rule: If any vertical line cuts graph at MORE than one point → NOT a function
TYPES OF FUNCTION – REMEMBER THIS
One-One: Different inputs → different outputs Many-One: Different inputs → same output Onto: Range = Codomain Into: Range ⊂ Codomain.
Some Important Questions
Q1. Ordered Pair
Find the values of x and y if
(2x−3,y+5)=(7,11)(2x − 3, y + 5) = (7, 11)(2x−3,y+5)=(7,11)
Solution:
First elements equal:
2x − 3 = 7
2x = 10
x = 5
Second elements equal:
y + 5 = 11
y = 6
Answer: x = 5, y = 6
Q2. Cartesian Product
If A = {1, 2, 3} and B = {4, 5}, find A × B.
Solution:
A × B = {(1,4), (1,5), (2,4), (2,5), (3,4), (3,5)}
Q3. Domain and Range
Find the domain and range of
R = {(1,2), (2,4), (3,6), (4,8)}
Solution:
Domain = {1, 2, 3, 4}
Range = {2, 4, 6, 8}
Q4. Inverse Relation
Find the inverse of
R = {(2,3), (4,5), (6,7)}
Solution:
Swap first and second elements:
R⁻¹ = {(3,2), (5,4), (7,6)}
Q5. Types of Relation
Check whether
R = {(1,2), (2,3), (3,4)}
is transitive.
Solution:
(1,2) and (2,3) ⇒ (1,3) not in R
(2,3) and (3,4) ⇒ (2,4) not in R
R is NOT transitive
Q6. Function or Not
Check whether
R = {(1,2), (2,4), (3,6), (2,8)}
is a function.
Solution:
Input 2 has two outputs (4 and 8).
Not a function.
Q7. Range of a Function
Find the range of
f(x) = 3x − 1
if domain D = {0, 1, 2, 3}
Solution:
f(0) = −1
f(1) = 2
f(2) = 5
f(3) = 8
Range = {−1, 2, 5, 8}
For further practice visit this link !!
https://besidedegree.com/exam/s/academic