Grade 9 Notes of Coordinate Geometry|| Optional Mathematics

Unit 4: Coordinate Geometry 

4.1 Locus

• Definition: Locus is the path traced by a moving point that satisfies a fixed condition (usually a circle or straight line).
• Steps to Find the Equation:
  1. Take a general point P(x, y) on the locus.
  2. Write the given condition as an algebraic expression.
  3. Simplify to get the equation in x and y.
• To Check a Point: Substitute the coordinates into the equation – if it satisfies, the point lies on the locus.
• 

Example:

• Distance from fixed point (-4, 5) is always 5 → circle (x + 4)² + (y - 5)² = 25 x² + y² + 8x - 10y + 16 = 0 (Pages 108–109 for figures).

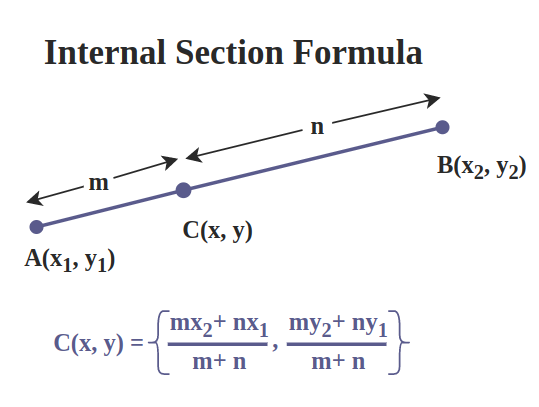
4.2 Section Formula

Internal Division (point inside the segment, ratio m:n):

• x = (m × x₂ + n × x₁) / (m + n)
• y = (m × y₂ + n × y₁) / (m + n)

Midpoint (ratio 1:1):

• x = (x₁ + x₂)/2
• y = (y₁ + y₂)/2

External Division (point outside the segment, ratio m:n):

• x = (m × x₂ - n × x₁) / (m - n)
• y = (m × y₂ - n × y₁) / (m - n)

Centroid (center of triangle):

• x = (x₁ + x₂ + x₃)/3
• y = (y₁ + y₂ + y₃)/3 (Page 121)

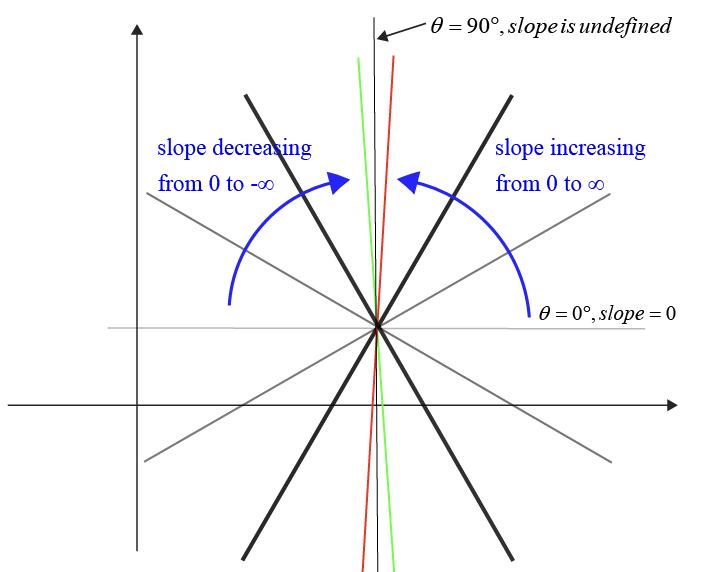
4.3 Slope of a Line

• Slope m = (y₂ - y₁)/(x₂ - x₁)
• Horizontal line: m = 0
• Vertical line: slope undefined
• Collinear Points: Same slope between any pairs

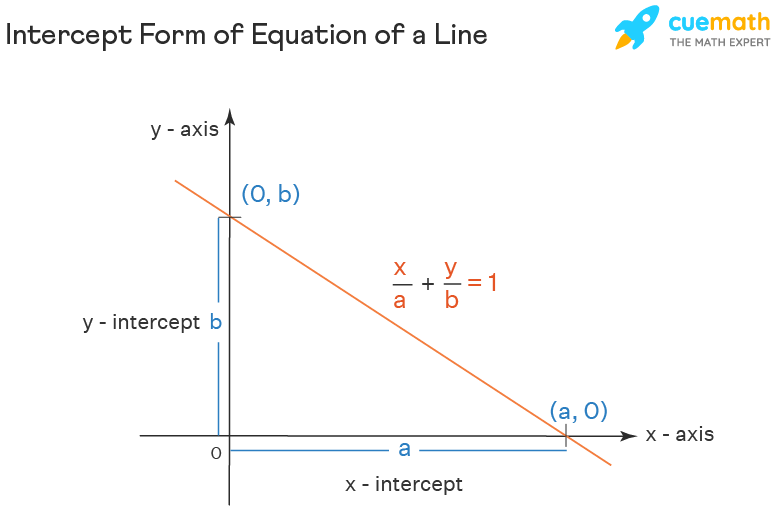
4.4 Equations of Straight Lines

1. Slope-Intercept: y = m x + c
2. Double Intercept: x/a + y/b = 1
3. Normal: x cos α + y sin α = p
4. Point-Slope: y - y₁ = m (x - x₁)
5. Two-Point: y - y₁ = (y₂ - y₁)/(x₂ - x₁) × (x - x₁)

Axes:

• x-axis: y = 0
• y-axis: x = 0

4.5 Conversion from General Form Ax + By + C = 0

• Slope: m = -A/B
• y-intercept: -C/B
• To normal form: Divide by √(A² + B²) and make RHS positive

4.6 Distance from Point to Line

• Formula: |A x₁ + B y₁ + C| / √(A² + B²)
• Between parallel lines: |C₁ - C₂| / √(A² + B²)

4.7 Area

Triangle: Area = (1/2) × |x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)|

• Area = 0 means collinear

Quadrilateral (vertices in order A→B→C→D→A): Area = (1/2) × |x₁y₂ - x₂y₁ + x₂y₃ - x₃y₂ + x₃y₄ - x₄y₃ + x₄y₁ - x₁y₄| 

Most Important Solved Questions 

Q1. Locus: Distance from fixed point (-4, 5) is always 5.
or, Take point P(x, y)
or, Distance formula: √[(x + 4)² + (y - 5)²] = 5
or, Square both sides: (x + 4)² + (y - 5)² = 25
or, Expand: x² + 8x + 16 + y² - 10y + 25 = 25
or, Subtract 25: x² + y² + 8x - 10y + 16 = 0

Q2. Point divides (-1, 3) & (8, 7) internally in ratio 2:5
or, x = (2×8 + 5×(-1)) / (2+5)
or,   = (16 - 5) / 7
or,   = 11/7
or, y = (2×7 + 5×3) / 7
or,   = (14 + 15) / 7
or,   = 29/7
or, Answer: (11/7, 29/7)

Q3. Midpoint of (4, -12) & (6, 8)
or, x = (4 + 6)/2
or,   = 10/2
or,   = 5
or, y = (-12 + 8)/2
or,   = (-4)/2
or,   = -2
or, Answer: (5, -2)

Q4. Line through (3, -2) with slope 1
or, Point-slope form: y - (-2) = 1(x - 3)
or, y + 2 = x - 3
or, x - y - 5 = 0

Q5. Double intercept: x-intercept 4, y-intercept -3
or, Form: x/4 + y/(-3) = 1
or, x/4 - y/3 = 1
or, Multiply by 12: 3x - 4y = 12

Q6. Normal form of 3x + 4y - 12 = 0
or, √(9 + 16) = 5
or, Divide by 5: (3/5)x + (4/5)y = 12/5
or, cos α = 3/5, sin α = 4/5, p = 12/5

Q7. Distance from (-3, -4) to 3x + 4y - 7 = 0
or, |3(-3) + 4(-4) - 7| / 5
or, |-9 - 16 - 7| / 5
or, |-32| / 5
or, 32/5

Q8. Area of triangle (0,7), (1,3), (5,5)
or, (1/2) |0(3-5) + 1(5-7) + 5(7-3)|
or, (1/2) |0 - 2 + 20|
or, (1/2) × 18
or, 9 square units

Q9. Show (3,4), (7,8), (11,12) collinear
or, Slope AB = (8-4)/(7-3) = 4/4 = 1
or, Slope BC = (12-8)/(11-7) = 4/4 = 1
or, Same slope → collinear

Q10. Centroid of (1,1), (1,7), (7,1)
or, x = (1 + 1 + 7)/3
or,   = 9/3
or,   = 3
or, y = (1 + 7 + 1)/3
or,   = 9/3
or,   = 3
or, Answer: (3, 3)

Q11.

Show that A (-4, 9), B (6, 9), C (7, 0) and D (–3, 0) are the vertices of a parallelogram.

Step 1: Midpoint of AC A (-4, 9), C (7, 0) x = (-4 + 7)/2 = 3/2 y = (9 + 0)/2 = 9/2 Midpoint of AC = (3/2, 9/2)

Step 2: Midpoint of BD B (6, 9), D (-3, 0) x = (6 + (-3))/2 = 3/2 y = (9 + 0)/2 = 9/2 Midpoint of BD = (3/2, 9/2)

Step 3: Conclusion Midpoint of AC = Midpoint of BD Therefore, diagonals bisect each other Hence, ABCD is a parallelogram.

Q12.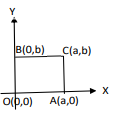

(A) If ABCD be a parallelogram with vertices A(10, 6), B (0, –1), C (2, –5) and D (x, y). Find coordinates of D.

Solution,

In parallelogram ABCD, vector AB = vector DC and vector AD = vector BC.
Easiest: D = A + (C - B) or D = B + C - A (standard formula).
or, D_x = B_x + C_x - A_x
or,   = 0 + 2 - 10
or,   = -8
or, D_y = B_y + C_y - A_y
or,   = -1 + (-5) - 6
or,   = -12
or, Coordinates of D: (-8, -12)

or, D_x = B_x + C_x - A_x or, = 0 + 2 - 10 or, = -8 or, D_y = B_y + C_y - A_y or, = -1 + (-5) - 6 or, = -12 or, Coordinates of D: (-8, -12)

 (B) In adjoining figure the coordinates of O, A, C and B are given. Show that OACB is a rectangle.

Solution Given (from figure):
O(0,0), A(a,0), B(0,b), C(a,b)
Solution:
To prove OACB is a rectangle:

All angles 90° or opposite sides equal and adjacent sides perpendicular.

or, Sides:
or, OA from O(0,0) to A(a,0) → along x-axis (horizontal)
or, OB from O(0,0) to B(0,b) → along y-axis (vertical)
or, OC from O(0,0) to C(a,b) → diagonal
or, AB from A(a,0) to B(0,b)
or, Check angles at O: OA horizontal, OB vertical → angle AOB = 90°
or, At A: OA horizontal, AC from A(a,0) to C(a,b) vertical → 90°
or, At C: CA vertical, CB from C(a,b) to B(0,b) horizontal → 90°
or, At B: BO vertical, BA horizontal → 90°
or, Opposite sides: OA = CB = a (length), OB = AC = b (length)
or, All angles 90° and opposite sides equal
or, Therefore, OACB is a rectangle.

For further practice visit this link !!

https://besidedegree.com/exam/s/academic