Matrices – 3.0 Review
Matrices are widely used in mathematics. The simplest but important application is to present data in rectangular arrangements for decision making.
Example – Grade Sheet of a Student:
SubjectCredit hourTotal GPObtained GPHighest GP of classNepali54.03.53.8Mathematics54.04.04.0English54.03.83.9Science54.03.94.0Social Study54.03.73.8HPE54.03.83.9Optional Maths54.03.94.0Rows represent subjects.
Columns represent credit hour, total GP, obtained GP, highest GP.
Questions:
a) Which row represents Social Studies? → 5th row
b) Which column represents Obtained GP? → 4th column
c) Highest GP in Science? → 4.0
Matrix Representation:
M = 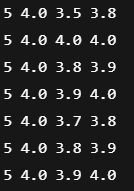
M = [
5 4.0 3.5 3.8
5 4.0 4.0 4.0
5 4.0 3.8 3.9
]
Number of rows = 3
Number of columns = 4
Order of M = 3×4
3.1 Matrix Elements
An element in row i and column j is denoted as a_ij.
Example:
A = [
a11 a12 a13
a21 a22 a23
]
a23 = element in 2nd row, 3rd column
a32 = element in 3rd row, 2nd column (if matrix has 3 rows)
3.2 Types of Matrices
TypeDefinitionExampleRow matrix1 rowA = [0 1 -3]Column matrix1 columnB = [3; -2; 1]Square matrixRows = ColumnsS = [[-2,4,6],[1,3,-5],[3,7,-9]]Rectangular matrixRows ≠ ColumnsP = [[1,2,3],[-2,4,-6]]Zero (null) matrixAll elements zeroO = [[0,0],[0,0]]Diagonal matrixNon-zero elements on main diagonal, others zeroD = [[1,0],[0,2]]Scalar matrixDiagonal elements equalS = [[2,0],[0,2]]Identity matrixScalar matrix with 1s on diagonalI = [[1,0],[0,1]]Triangular matrixUpper/lower triangularU = [[1,2],[0,3]] ; L = [[1,0],[2,3]]Symmetric matrixA = A^TS = [[x,y],[y,z]]3.3 Operations on Matrices
Addition
Matrices must have the same order.
Add corresponding elements.
Example:
A = [
3 7
11 13
],
B = [
2 4
8 10
]
A + B = [
5 11
19 23
]
Properties of Addition:
Commutative: A + B = B + A
Associative: (A + B) + C = A + (B + C)
Identity: A + O = A
Additive inverse: A + (-A) = O
Subtraction
Subtract corresponding elements.
Not commutative: A − B ≠ B − A
Scalar Multiplication
Multiply each element by a scalar k:
kA = k * [
a b
c d
] = [
ka kb
kc kd
]
Matrix Multiplication
Condition: Number of columns of first = Number of rows of second
Element at position (i,j) = row_i × column_j
Not commutative: AB ≠ BA
Example:
A = [
5 8
2 -3
],
B = [
7 -4
3 2
]
AB = [
59 -4
15 -14
],
BA = [
27 68
9 18
]
3.4 Transpose of a Matrix
Transpose (A^T) = Interchange rows and columns
Properties:
(A^T)^T = A
(A + B)^T = A^T + B^T
(kA)^T = kA^T
Important Questions & Solutions
Q1. Find 2A if
A = [ 3 5 7
1 0 -2 ]
Solution:
Multiply each element by 2:
2A = [ 6 10 14
2 0 -4 ]
Q2. Find the sum of the matrices
A = [ 1 2
3 4 ], B = [ 2 0
1 3 ]
Solution:
Add corresponding elements:
A + B = [ 1+2 2+0
3+1 4+3 ]
= [ 3 2
4 7 ]
Q3. Find the difference of the matrices
A = [ 1 2
3 4 ], B = [ 2 0
1 3 ]
Solution:
Subtract corresponding elements:
A - B = [ 1-2 2-0
3-1 4-3 ]
= [ -1 2
2 1 ]
Q4. Find the transpose of the matrix
A = [ 1 2
3 4 ]
Solution:
Swap rows and columns:
A^T = [ 1 3
2 4 ]
Q5. Find the product of the matrices
A = [ 1 2
3 4 ], B = [ 2 0
1 3 ]
Solution:
Multiply row of A with column of B:
AB = [ (1*2 + 2*1) (1*0 + 2*3)
(3*2 + 4*1) (3*0 + 4*3) ]
= [ 4 6
10 12 ]
Q6. Find 3A if
A = [ 1 0 2
-1 3 1 ]
Solution:
Multiply each element by 3:
3A = [ 3 0 6
-3 9 3 ]
Q7. Find the product of matrices
A = [ 1 2 3
4 5 6 ], B = [ 7 8
9 10
11 12 ]
Solution:
Multiply row of A with column of B:
AB = [ (1*7 + 2*9 + 3*11) (1*8 + 2*10 + 3*12)
(4*7 + 5*9 + 6*11) (4*8 + 5*10 + 6*12) ]
= [ 58 64
139 154 ]
Q8. Find 2A - B if
A = [ 1 2
3 4 ], B = [ 0 1
1 0 ]
Solution:
Step 1: Multiply A by 2 → 2A = [2 4 ; 6 8]
Step 2: Subtract B → 2A - B = [2-0 4-1 ; 6-1 8-0]
2A - B = [ 2 3
5 8 ]
Q9. Check if the matrix
A = [ 1 0 0
0 1 0
0 0 1 ]
is an identity matrix.
Solution:
Identity matrix has 1s on the diagonal and 0s elsewhere.
A is an identity matrix.
Q10. Check if the matrix
A = [ 1 2
2 4 ]
is symmetric.
Solution:
Transpose A^T = [1 2 ; 2 4] → same as A
A is symmetric.
For further practice visit this link !!
https://besidedegree.com/exam/s/academic