Statistics – Chapter 8 Study Guide
8.0 Review of Statistics
Data: Collection of facts, numbers, or observations.
Types of Data:
Individual data: Each observation is considered separately.
Discrete data: Data that can take specific, separate values.
Frequency: Number of times a particular value occurs.
Cumulative frequency: Running total of frequencies up to a certain point.
Arithmetic Mean (Average):
X̄ = ΣX / N
Measures of Central Tendency:
Mean (X̄): Average of all values.
Median (Md): Middle value of ordered data.
Mode: Most frequently occurring value.
8.1 Partition Values of Ungrouped Data
Partition values: Divide data into more than two parts.
(i) Quartiles
Divide data into 4 equal parts: Q1, Q2 (median), Q3
Formulas for individual/discrete data:
Q1 = (N + 1)/4 th item
Q2 = (N + 1)/2 th item
Q3 = 3(N + 1)/4 th item
Example:
Data: 22, 26, 14, 30, 18, 17, 35, 41, 12, 32, 34
Ascending: 12, 14, 17, 18, 22, 26, 30, 32, 34, 35, 41
N = 11
Q1 = 3rd item = 17
Q3 = 9th item = 34
(ii) Deciles
Divide data into 10 equal parts: D1, D2, …, D9
Formula:
Dn = n(N + 1)/10 th item, n = 1, 2, …, 9
Example:
Data: 25, 27, 28, 29, 30, 31, 38, 40, 45, 52, 59
D7 = 7(12)/10 = 8.4 th item = 40 + 0.4(45 – 40) = 42
(iii) Percentiles
Divide data into 100 equal parts: P1, P2, …, P99
Formula:
Pn = n(N + 1)/100 th item, n = 1, 2, …, 99
Example:
P45 = 45 * 12 / 100 = 5.4 th item = 30 + 0.4(31 – 30) = 30.4
8.2 Measures of Dispersion
Dispersion: Measures how spread out the data is.
Common measures:
Range
Quartile Deviation (QD)
Mean Deviation (MD)
Variance (σ²)
Standard Deviation (SD)
Coefficients of Dispersion
1. Quartile Deviation (QD)
QD = (Q3 – Q1)/2
Coefficient of Quartile Deviation (CQD):
CQD = (Q3 – Q1) / (Q3 + Q1)
Example:
Q1 = 17, Q3 = 34
QD = (34 – 17)/2 = 8.5
CQD = (34 – 17)/(34 + 17) = 17/51 ≈ 0.33
2. Mean Deviation (MD)
Mean of absolute deviations from mean or median
From mean: MD = Σ|X – X̄| / N
From median: MD = Σ|X – Md| / N
Coefficient of Mean Deviation (CMD):
CMD = MD / Mean or Median
Example:
Data: 40, 44, 54, 60, 62, Median = 54
Σ|X – Md| = 38, N = 5
MD = 38 / 5 = 7.6
CMD = 7.6 / 54 ≈ 0.14
3. Standard Deviation (SD)
SD = σ = √(Σ(X – X̄)² / N)
For discrete series:
SD = √(Σf(X – X̄)² / N)
Coefficient of SD (CSD):
CSD = SD / X̄
Example:
Data: 22, 25, 30, 35, 40, 45, 48
X̄ = 35, Σ(X – X̄)² = 588
SD = √(588/7) = 9.17
CSD = 9.17 / 35 ≈ 0.262
4. Variance
Variance = σ² = Σ(X – X̄)² / N
Coefficient of Variation (CV):
CV = SD / X̄
5. Important Solved Questions
Q1. Find Quartiles of the data:
Data: 12, 14, 17, 18, 22, 26, 30, 32, 34, 35, 41
Solution:
Arrange in ascending order (already arranged)
N = 11
Q1 = (N + 1)/4 th item = 12/4 = 3rd item = 17
Q2 (Median) = (N + 1)/2 th item = 12/2 = 6th item = 26
Q3 = 3(N + 1)/4 th item = 36/4 = 9th item = 34
Answer: Q1 = 17, Median = 26, Q3 = 34
Q2. Find D7 (7th decile) of the data:
Data: 25, 27, 28, 29, 30, 31, 38, 40, 45, 52, 59
Solution:
N = 11
D7 = 7(N + 1)/10 th item = 7 * 12 / 10 = 8.4 th item
8th item = 40, 9th item = 45
Interpolate: 40 + 0.4(45 – 40) = 40 + 2 = 42
Answer: D7 = 42
Q3. Find P45 (45th percentile) of the data:
Data: 25, 27, 28, 29, 30, 31, 38, 40, 45, 52, 59
Solution:
N = 11
P45 = 45(N + 1)/100 th item = 45 * 12 / 100 = 5.4 th item
5th item = 30, 6th item = 31
Interpolate: 30 + 0.4(31 – 30) = 30 + 0.4 = 30.4
Answer: P45 = 30.4
Q4. Find Mean Deviation from Median:
Data: 40, 44, 54, 60, 62
Solution:
Median Md = 54
Σ|X – Md| = |40 – 54| + |44 – 54| + |54 – 54| + |60 – 54| + |62 – 54| = 14 + 10 + 0 + 6 + 8 = 38
N = 5
MD = 38 / 5 = 7.6
CMD = MD / Median = 7.6 / 54 ≈ 0.14
Answer: MD = 7.6, CMD ≈ 0.14
Q5. Find Standard Deviation and CSD:
Data: 22, 25, 30, 35, 40, 45, 48
Solution:
Mean X̄ = (22 + 25 + 30 + 35 + 40 + 45 + 48)/7 = 245/7 = 35
Σ(X – X̄)² = (22–35)² + (25–35)² + (30–35)² + (35–35)² + (40–35)² + (45–35)² + (48–35)²
= 169 + 100 + 25 + 0 + 25 + 100 + 169 = 588
SD = √(588 / 7) = √84 ≈ 9.17
CSD = SD / X̄ = 9.17 / 35 ≈ 0.262
Answer: SD ≈ 9.17, CSD ≈ 0.262
Q6 Table solution
Data Table:
Fig 1: Table
Step 1: Total Frequency
N = 2 + 3 + 5 + 4 + 1 = 15
Step 2: Mean
fX = f * X
Fig2:Table
Sum fX = 20 + 36 + 75 + 72 + 20 = 223
Mean = sum fX / N = 223 / 15 ≈ 14.87
Step 3: Median
Cumulative frequency (CF):
Fig 3 :Table
Median position = N/2 = 15/2 = 7.5th item → lies in X = 15
Median = 15
Step 4: Mean Deviation from Median (MD)
| X | f | |X - Md| | f * |X - Md||
| 10 | 2 | 5 | 10 |
| 12 | 3 | 3 | 9 |
| 15 | 5 | 0 | 0 |
| 18 | 4 | 3 | 12 |
| 20 | 1 | 5 | 5 |
Sum f * |X - Md| = 36
MD = 36 / 15 = 2.4
CMD = MD / Median = 2.4 / 15 = 0.16
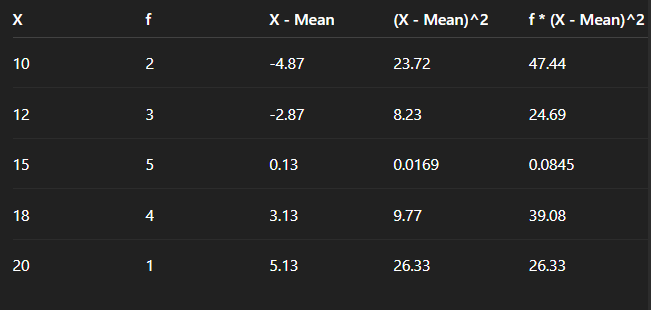
Step 5: Standard Deviation (SD)
Fig 4: Table
Sum f * (X - Mean)^2 ≈ 137.63
SD = sqrt(137.63 / 15) = sqrt(9.175) ≈ 3.03
CSD = SD / Mean = 3.03 / 14.87 ≈ 0.204
Final Answers:
Mean = 14.87
Median = 15
MD = 2.4
CMD = 0.16
SD = 3.03
CSD = 0.204
For further practice visit this link !!
https://besidedegree.com/exam/s/academic
Gallery
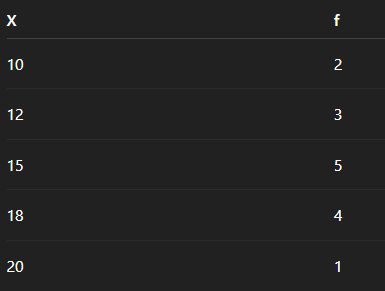
Fig 1
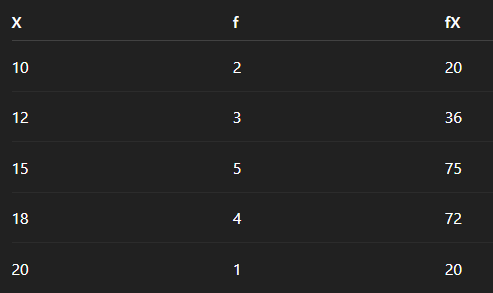
Fig 2
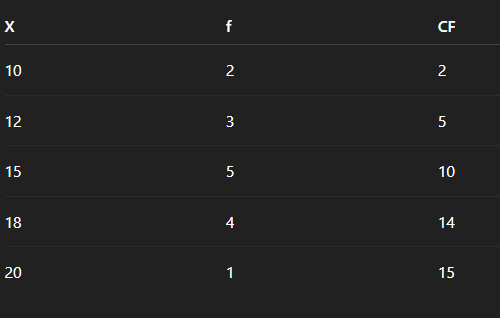
Fig 3