Unit 7: Transformations

7.0 What is Transformation?

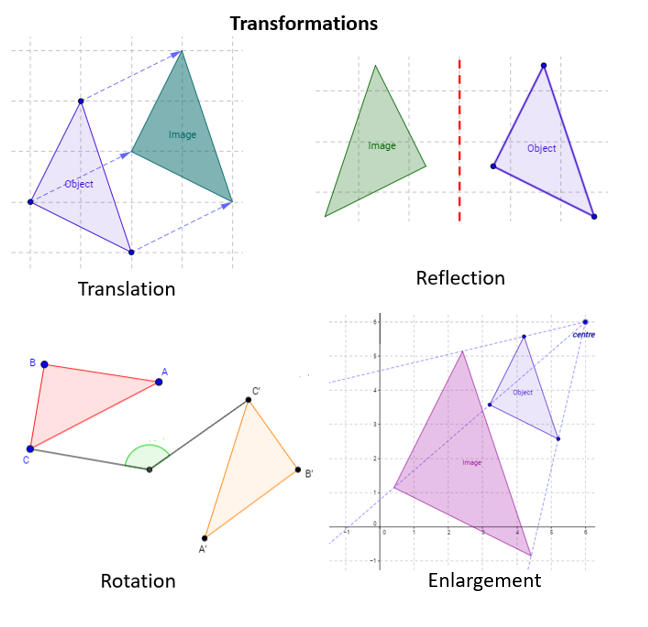
A transformation is a change in the position, orientation, or size of a geometric object.

The original object is called the object.

The result of the transformation is called the image.

Types of Transformation:

Isometric Transformation: Object and image are congruent (same size and shape).

Examples: Reflection, Rotation, Translation

Non-Isometric Transformation: Object and image are similar (shape same, size changes).

Example: Enlargement

7.1 Reflection

Definition:
A reflection is a transformation where a figure is flipped across a line called the axis of reflection. The perpendicular distance from the line to each point of the object and its image is equal.

Properties:

Points on the mirror line are invariant.

Reflection preserves lengths and angles (congruent).

Object and image are mirror-reverse of each other.

Lines perpendicular to the mirror line are invariant, but points on them are not.

Examples in Daily Life:

Mirror reflection of your face.

Reflection in calm water.

Rearview mirrors in vehicles.

Reflection in Cartesian Plane

Axis / LineImage of P(x, y)x-axis (y=0)(x, –y)y-axis (x=0)(–x, y)y = x(y, x)y = –x(–y, –x)x = a(2a – x, y)y = b(x, 2b – y)

Examples:

Point (4, –2) reflected in x-axis → (4, 2)

Point (3, 1) reflected in y = –x → (–1, –3)

7.2 Rotation

Definition:
A rotation moves a figure around a fixed point called the centre of rotation by a certain angle of rotation. Each point remains at a constant distance (radius) from the center.

Properties:

Centre of rotation is invariant.

Distances from the centre are preserved.

Object and image are congruent.

Perpendicular bisector of the segment joining a point and its image passes through the centre.

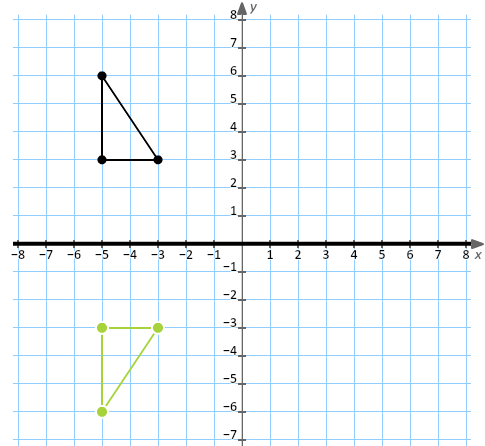
Rotation about the Origin (0,0)

Fig2 : Table

Rotation about a Point (a,b)

Fig3 : Table

Examples:

Point (–2, 4) rotated –90° about origin → (4, 2)

Point (1, –3) rotated 270° about origin → (–3, –1)

Fig 1

7.3 Translation

Definition:
Translation moves every point of an object by the same distance and direction, defined by a vector.

Properties:

Object and image are congruent.

Each point moves equally along the vector.

Translation is a direct isometric transformation.

Translation in Cartesian Plane

Definition:
Slide a figure along a vector.

Properties:

Object and image are congruent.

Each point moves the same distance in the same direction.

Translation Rule:
If a point is P(x,y)P(x, y)P(x,y) and the translation vector is T⃗=(a,b)\vec{T} = (a, b)T=(a,b), then:

P(x,y)→P′(x+a,y+b)P(x, y) \to P'(x + a, y + b)P(x,y)→P′(x+a,y+b)

Examples:

Point (2, 3) translated by T⃗=(4,0)\vec{T} = (4, 0)T=(4,0):

P′(2,3)=(2+4,3+0)=(6,3)P'(2, 3) = (2 + 4, 3 + 0) = (6, 3)P′(2,3)=(2+4,3+0)=(6,3)

Point (3, –4) translated by T⃗=(−4,3)\vec{T} = (-4, 3)T=(−4,3):

P′(3,−4)=(3−4,−4+3)=(−1,−1)P'(3, -4) = (3 - 4, -4 + 3) = (-1, -1)P′(3,−4)=(3−4,−4+3)=(−1,−1)

7.4 Enlargement (Scaling)

Definition:
Enlargement is a transformation that changes the size of a figure but keeps the shape same. The fixed point is called the centre of enlargement.

Scale factor > 1 → Enlargement (bigger)

Scale factor < 1 → Reduction (smaller)

Formula:
If the centre of enlargement is O(0,0) and scale factor k, then

Image of P(x, y) → P'(kx, ky)

Coordinates Quick Reference

Reflection:

x-axis → (x, –y)

y-axis → (–x, y)

y = x → (y, x)

y = –x → (–y, –x)

Rotation about origin:

+90° → (–y, x)

+180° → (–x, –y)

+270° → (y, –x)

Translation:

Vector (a, b) → (x + a, y + b)

Enlargement:

Scale k → (kx, ky)

Important Questions

Q1: Reflect the points A(3,5) and B(–2,–1) in the x-axis and y-axis.

Solution:

, Step 1: Reflection in x-axis:
A(3,5) → (3, –5)
B(–2,–1) → (–2, 1)

, Step 2: Reflection in y-axis:
A(3,5) → (–3, 5)
B(–2,–1) → (2, –1)

Q2: Rotate P(4,2) and Q(–3,–2) through 90° about the origin.

Solution:

, Step 1: Use rotation formula for +90°: (x, y) → (–y, x)
P(4,2) → (–2, 4)
Q(–3,–2) → (2, –3)

Q3: Translate R(2,3) by vector (4,0) and S(–1,–2) by vector (–2,3).

Solution:

, Step 1: Translation formula: P(x, y) → (x + a, y + b)
R(2,3) by (4,0) → (2+4, 3+0) → (6,3)

, Step 2: S(–1,–2) by (–2,3) → (–1–2, –2+3) → (–3,1)

Q4: Find the image of P(2,3) under enlargement with centre O(0,0) and scale factor 2.

Solution:

, Step 1: Use enlargement formula: P(x, y) → (kx, ky)
, Step 2: P(2,3) → (2×2, 2×3) → (4,6)

Q5: Reflect P(3,4) in y = x, then rotate the image 180° about origin.

Solution:

, Step 1: Reflection in y = x: P(3,4) → (4,3)

, Step 2: Rotation 180° about origin: (x, y) → (–x, –y)
(4,3) → (–4, –3)

Q6: Translate A(–2,5) by vector (3,–7), then reflect the image in x-axis.

Solution:

, Step 1: Translation: A(–2,5) → (–2+3, 5–7) → (1,–2)

, Step 2: Reflection in x-axis: (1,–2) → (1,2)

Q7: Rotate B(–1,2) 270° about origin, then enlarge with scale factor 3.

Solution:

, Step 1: Rotation 270°: (x, y) → (y, –x)
B(–1,2) → (2,1)

, Step 2: Enlargement with scale factor 3: (2,1) → (6,3)

For further practice visit this link !!

https://besidedegree.com/exam/s/academic