1. Definition
A set is a well-defined collection of distinct objects, called elements.
Notation: a ∈ A (a belongs to A), b ∉ A (b does not belong to A)
Example:
A = {2,4,6,8} → 2 ∈ A, 5 ∉ A
2. Ways to Represent Sets
Roster/Formal Form: List all elements
Example: A = {2,4,6,8}
Set-Builder Form: Describe elements using a property
Example: A = {x : x is an even number less than 10}
Example:
B = {x : x is a prime number < 10} = {2,3,5,7}
3. Types of Sets
TypeDescriptionExampleFinite setHas countable elements{1,2,3}Infinite setCannot be counted{1,2,3,...}Empty set / NullNo elements{} or ΦSingleton setOne element{5}Equal setsSame elements{1,2} = {2,1}Universal setContains all elements under discussionU = {1,2,3,4,5,6,7,8,9,10}
4. Subsets
A ⊆ B → every element of A is in B
Proper subset: A ⊂ B (A ≠ B)
Empty set Φ is subset of every set
Number of subsets: 2^n
Number of proper subsets: 2^n - 1
Example:
A = {a,b,c} → subsets = {Φ, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}} → 8 subsets
5. Power Set
The power set of A, P(A), is the set of all subsets of A
n(P(A)) = 2^n, where n = number of elements in A
Example:
A = {1,2} → P(A) = {Φ, {1}, {2}, {1,2}}
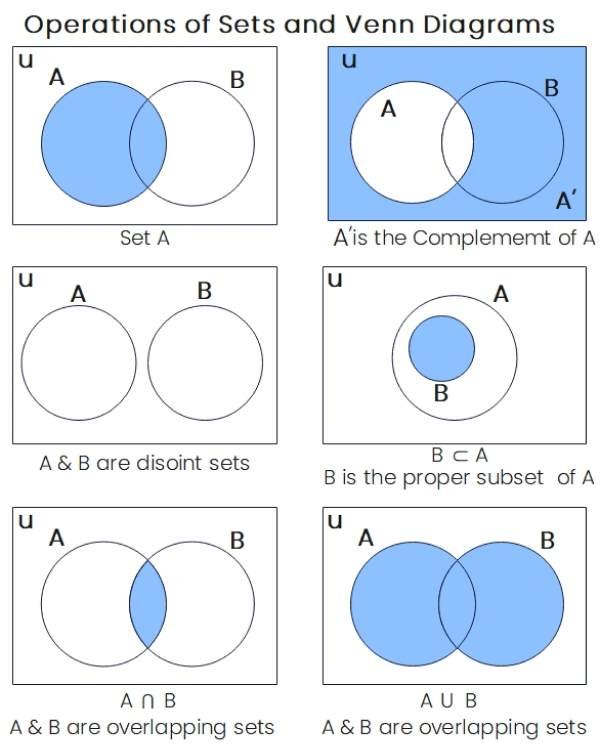
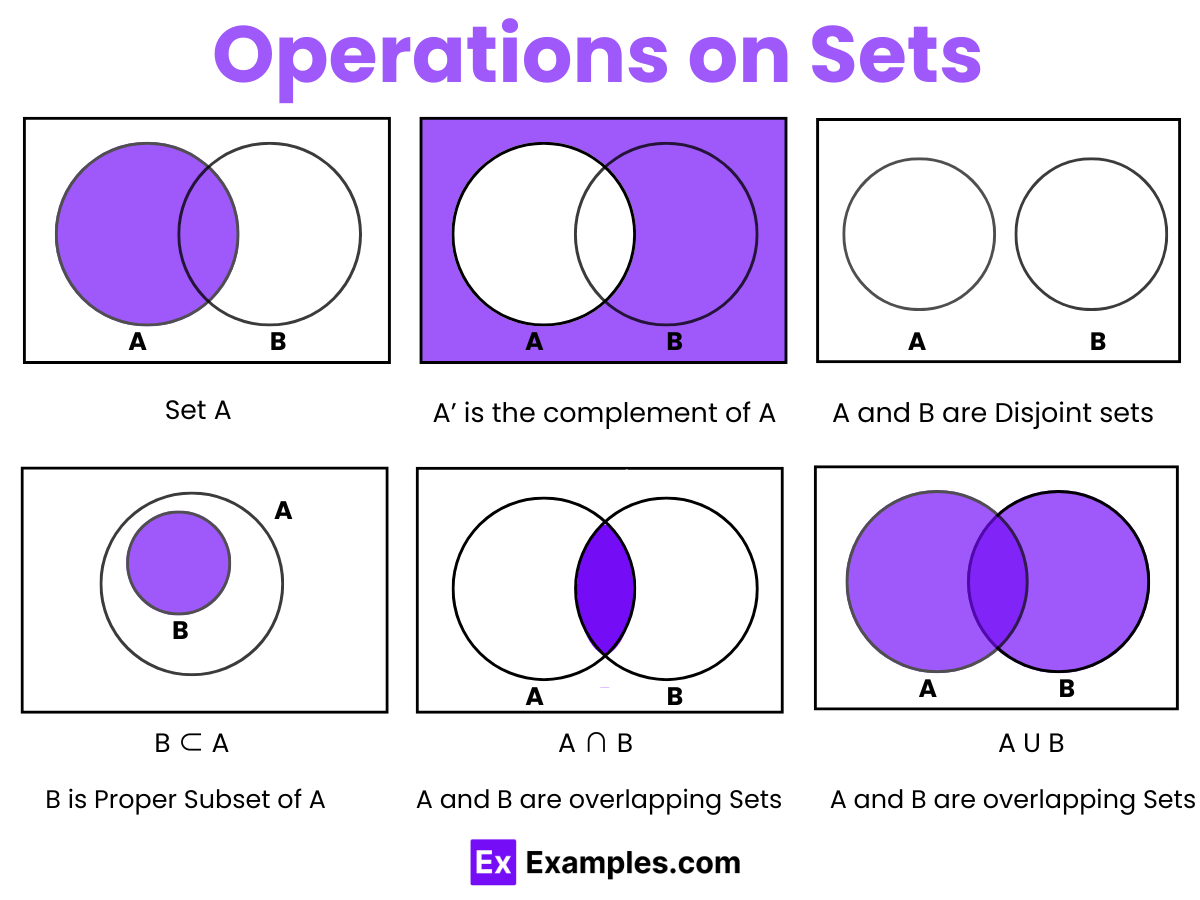
6. Venn Diagram & Set Operations
Union: A ∪ B → elements in A or B or both
Intersection: A ∩ B → elements common to A and B
Difference: A - B → elements in A but not in B
Complement: A' → elements not in A, with respect to universal set U
Example:
A = {1,2,3,4}, B = {3,4,5,6}
A ∪ B = {1,2,3,4,5,6}
A ∩ B = {3,4}
A - B = {1,2}
7. Important Formulas
Two Sets:
n(A ∪ B) = n(A) + n(B) - n(A ∩ B)
n(A') = n(U) - n(A)
Three Sets:
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(C ∩ A) + n(A ∩ B ∩ C)
De Morgan’s Laws:
(A ∪ B)' = A' ∩ B'
(A ∩ B)' = A' ∪ B'
8. Real-Life Applications
Survey problems
Probability & counting
Data classification
Computer science (databases, search queries)
9. Commonly Asked Questions (Solved)
Q1: Write set-builder form for A = {2,4,6,8,10}
A = {2,4,6,8,10}
or A = {x : x is an even natural number ≤ 10}
Q2: Write roster form for B = {x : x is a prime number < 10}
B = {x : x is prime < 10}
or B = {2,3,5,7}
Q3: n(A) = 20, n(B) = 15, n(A ∩ B) = 5. Find n(A ∪ B)
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
or n(A ∪ B) = 20 + 15 – 5
or n(A ∪ B) = 30
Q4: U = {1,2,...,10}, A = {1,2,3,4}. Find A'
A' = U – A
or A' = {1,2,3,4,5,6,7,8,9,10} – {1,2,3,4}
or A' = {5,6,7,8,9,10}
Q5: Number of subsets of {a,b,c,d}
Number of subsets = 2^n
or n = 4 → 2^4
or Number of subsets = 16
Q6: A = {1,2,3}, B = {3,4,5}. Find A ∪ B, A ∩ B, A – B, B – A
A ∪ B = {1,2,3} ∪ {3,4,5}
or A ∪ B = {1,2,3,4,5}
A ∩ B = {1,2,3} ∩ {3,4,5}
or A ∩ B = {3}
A – B = {1,2,3} – {3,4,5}
or A – B = {1,2}
B – A = {3,4,5} – {1,2,3}
or B – A = {4,5}
Q7: De Morgan’s Law Example: U = {1,2,3,4,5}, A = {1,2}, B = {2,3}
(A ∪ B)' = U – (A ∪ B)
or A ∪ B = {1,2,3}
or (A ∪ B)' = {4,5}
A' ∩ B' = (U – A) ∩ (U – B)
or A' = {3,4,5}, B' = {1,4,5}
or A' ∩ B' = {4,5}
(A ∪ B)' = A' ∩ B'
Q8: U = {1,2,...,10}, A = {1,2,3,4}, B = {3,4,5,6}. Find n(A ∪ B)
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
or n(A ∪ B) = 4 + 4 – 2
or n(A ∪ B) = 6
Q9: Three sets: n(A) = 10, n(B) = 8, n(C) = 12, n(A ∩ B) = 3, n(B ∩ C) = 2, n(C ∩ A) = 4, n(A ∩ B ∩ C) = 1. Find n(A ∪ B ∪ C)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A) + n(A ∩ B ∩ C)
or n(A ∪ B ∪ C) = 10 + 8 + 12 – 3 – 2 – 4 + 1
or n(A ∪ B ∪ C) = 22
Q10: In a class of 40 students, 25 like football, 18 like cricket, 10 like both. Find students who like either football or cricket
n(F ∪ C) = n(F) + n(C) – n(F ∩ C)
or n(F ∪ C) = 25 + 18 – 10
or n(F ∪ C) = 33
Q11: In a class of 30 students, 18 like tea, 12 like coffee, 5 like both. Find students who like neither
n(Tea ∪ Coffee) = n(Tea) + n(Coffee) – n(Tea ∩ Coffee)
or n(Tea ∪ Coffee) = 18 + 12 – 5
or n(Tea ∪ Coffee) = 25
or Students who like neither = 30 – 25
or Students = 5
Visit this link for further practice!!
Gallery