C0-ORDINATE GEOMETRY

• Graph with Points A, B, C, D: Four points forming a quadrilateral (typically on grid).
• Tasks:
  • Equation of lines AB, BC, CD, AD: Use two-point form.
  • Slopes: m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}m=x2​−x1​y2​−y1​​.
    • Parallel to x-axis: m = 0.
    • Parallel to y-axis: m undefined.
    • Slope same in either direction.
• Straight Line Equation:
  • Satisfies coordinates on line only.
  • Point-slope: y−y1=m(x−x1)y - y_1 = m(x - x_1)y−y1​=m(x−x1​).
  • Two-point: y−y1=y2−y1x2−x1(x−x1)y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1)y−y1​=x2​−x1​y2​−y1​​(x−x1​).

4.1 Angle Between Two Straight Lines

• Slope and Inclination: m = tan θ.
• Angle θ Between Lines (slopes m₁, m₂):
  • tan⁡θ=∣m1−m21+m1m2∣\tan \theta = \left| \frac{m_1 - m_2}{1 + m_1 m_2} \right|tanθ=​1+m1​m2​m1​−m2​​​ (acute angle usually with absolute value; ± for both).
  • Acute if numerator/magnitude positive in context; obtuse opposite.
  • Parallel: m₁ = m₂ (θ = 0° or 180°).
  • Perpendicular: m₁ m₂ = -1.
• General Lines: a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0.
  • Slopes: m₁ = -a₁/b₁, m₂ = -a₂/b₂.
  • tan⁡θ=∣a1b2−a2b1a1a2+b1b2∣\tan \theta = \left| \frac{a_1 b_2 - a_2 b_1}{a_1 a_2 + b_1 b_2} \right|tanθ=​a1​a2​+b1​b2​a1​b2​−a2​b1​​​.
  • Parallel: a₁/a₂ = b₁/b₂ (≠ c₁/c₂).
  • Perpendicular: a₁a₂ + b₁b₂ = 0.
• Applications:
  • Parallel line through point: Same slope.
  • Perpendicular line: Slope = -1/m.
  • Lines at given angle (e.g., 60°, 45°): Solve for m using tan formula (two lines).
  • Perpendicular bisector: Midpoint + slope = -1/original.
  • Diagonals of square: Intersect at midpoint, perpendicular.

4.2 Equation of Pair of Straight Lines

• Homogeneous Second Degree: ax² + 2hxy + by² = 0 (pair through origin).
• Formation: Product of lines y = m₁x, y = m₂x → y² - (m₁ + m₂)xy + m₁ m₂ x² = 0.
• Angle Between Pair:
  • tan⁡θ=∣2h2−aba+b∣\tan \theta = \left| \frac{2 \sqrt{h^2 - ab}}{a + b} \right|tanθ=​a+b2h2−ab​​​.
  • Perpendicular: a + b = 0.
  • Parallel/Coincident: h² = ab.
• Separate Lines: Factorize or solve as quadratic in (y/x).
• Combined Equation: Multiply individual lines through origin.
• Perpendicular to Given Pair: Find original slopes, take reciprocals negative, combine.

4.3 Conic Sections

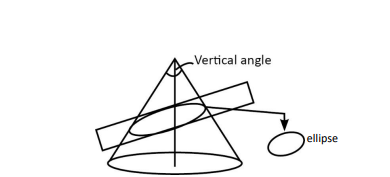
• Right Circular Cone: Vertex O, axis (vertical), generator (slant), base.
• Sections:
  • Circle: Plane || base.
  • Parabola: Plane || generator.
  • Ellipse: Plane angle > vertical angle but <90°.
  • Hyperbola: Plane || axis (double cone).
  • 

4.4 Circle

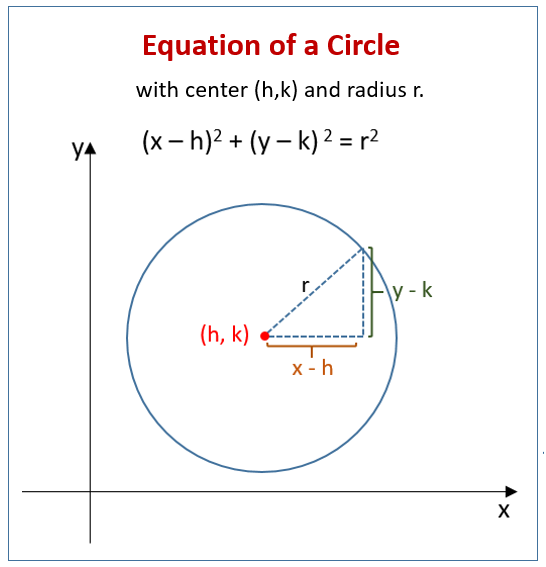
• Definition: Locus of point at fixed distance r from centre.
• Equations:
  • Centre (0,0): x² + y² = r².
  • Centre (h,k): (x - h)² + (y - k)² = r².
  • Diameter ends (x₁,y₁), (x₂,y₂): (x - x₁)(x - x₂) + (y - y₁)(y - y₂) = 0.
  • General: x² + y² + 2gx + 2fy + c = 0 → centre (-g, -f), r = √(g² + f² - c).
• Centre/Radius: Complete square.
• Special:
  • Through 3 points: Equidistant centre (solve system).
  • Touching axes: Centre (r,r) etc., r = distance to axis.
  • Centre on line + through point: Use distance.
  • Concyclic: 4 points on one circle.
  • Angle in semicircle: 90°.

Question 1
Find the equation of the line passing through (2, 3) and parallel to
4x - 5y + 10 = 0.

Solution:
Given line: 4x - 5y + 10 = 0
Rewrite in slope form:

5y = 4x + 10
y = (4/5)x + 2

So slope m = 4/5

For a parallel line, slope remains same.
Using point-slope form:

y - 3 = (4/5)(x - 2)

Multiply both sides by 5:

5y - 15 = 4x - 8

Rearranging:

4x - 5y + 7 = 0

Question 2
Find the acute angle between the lines
3x - 4y + 5 = 0 and 4x + 3y - 1 = 0.

Solution:
First line:

3x - 4y + 5 = 0
4y = 3x + 5
y = (3/4)x + 5/4

So slope m1 = 3/4

Second line:

4x + 3y - 1 = 0
3y = -4x + 1
y = (-4/3)x + 1/3

So slope m2 = -4/3

Formula for angle between two lines:

tan(theta) = |(m1 - m2) / (1 + m1m2)|

Substitute values:

tan(theta) = |(3/4 + 4/3) / (1 - 1)|

Denominator becomes zero.
Therefore theta = 90 degrees.

So the acute angle between the lines is 90 degrees.

Question 3
Find the combined equation of the pair of lines
x - y = 0 and 2x + y = 0.

Solution:
Combined equation is product of both equations:

(x - y)(2x + y) = 0

Multiply:

2x squared + xy - 2xy - y squared = 0

Simplify:

2x squared - xy - y squared = 0

Question 4
Find the equation of the circle with centre (3, -2) and radius 5.

Solution:
Standard form of circle:

(x - h) squared + (y - k) squared = r squared

Here h = 3, k = -2, r = 5

Substitute:

(x - 3) squared + (y + 2) squared = 25

Expand:

x squared - 6x + 9 + y squared + 4y + 4 = 25

Rearrange:

x squared + y squared - 6x + 4y - 12 = 0

Question 5
Find the centre and radius of the circle
x squared + y squared + 4x - 6y - 12 = 0.

Solution:
Group x and y terms:

(x squared + 4x) + (y squared - 6y) = 12

Complete square:

(x + 2) squared - 4 + (y - 3) squared - 9 = 12

Add constants:

(x + 2) squared + (y - 3) squared = 25

So,
Centre = (-2, 3)
Radius = 5

MORE PRACTICE QUESTIONS (MODERATE TO COMPLEX)

Question 6
Find equation of the line passing through (1, -2) and perpendicular to
2x + 3y - 7 = 0.

Solution:
Given line:

2x + 3y - 7 = 0
3y = -2x + 7
y = (-2/3)x + 7/3

Slope of given line = -2/3

Slope of perpendicular line = 3/2

Using point-slope form:

y + 2 = (3/2)(x - 1)

Multiply by 2:

2y + 4 = 3x - 3

Rearrange:

3x - 2y - 7 = 0

Question 7
Find the angle between lines
x + y = 0 and x - y = 0.

Solution:
First line slope = -1
Second line slope = 1

tan(theta) = |(-1 - 1) / (1 - 1)|

Denominator zero.
So angle = 90 degrees.

Question 8
Find combined equation of pair of lines passing through origin and having slopes 2 and -3.

Solution:
General equation:

(y - 2x)(y + 3x) = 0

Multiply:

y squared + 3xy - 2xy - 6x squared = 0

Simplify:

y squared + xy - 6x squared = 0

Question 9
Find the equation of circle passing through (0,0) with centre on x-axis and radius 5.

Solution:
Let centre be (a, 0).

Using circle equation:

(x - a) squared + y squared = 25

Since circle passes through origin:

a squared = 25

So a = 5 or a = -5

Hence equations:

(x - 5) squared + y squared = 25
or
(x + 5) squared + y squared = 25

Question 10
Find equation of circle passing through points (1,0), (0,1), and (0,-1).

Solution:
General circle equation:

x squared + y squared + 2gx + 2fy + c = 0

Substitute points one by one.

For (1,0):

1 + 0 + 2g + c = 0

For (0,1):

1 + 2f + c = 0

For (0,-1):

1 - 2f + c = 0

Subtract last two equations:

4f = 0
So f = 0

Then c = -1

Then 2g = 0
So g = 0

Final equation:

x squared + y squared - 1 = 0

Visit this link for further practice!!

https://besidedegree.com/exam/s/academic