Transformation

7.0 Review: Types of Transformations

Concept Clarification: Transformation refers to changing the position, size, or orientation of a geometric figure while preserving certain properties (e.g., distances in rigid transformations). It maps an object to its image.

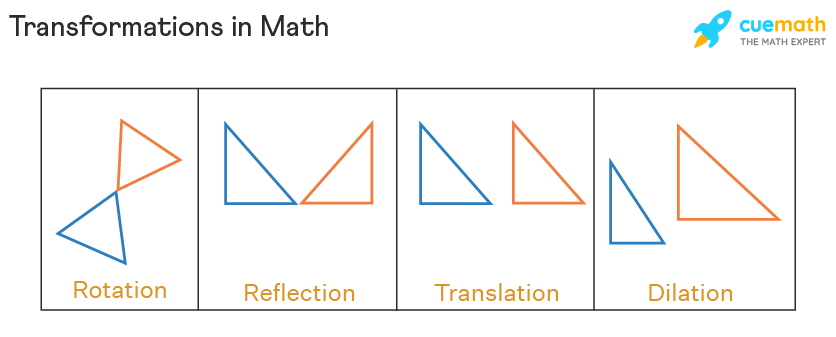
Types of Transformations (Discuss in group: Reflection, Rotation, Translation, Enlargement from previous classes):

• Reflection (Flip): Mirror image over a line (axis of reflection). Points equidistant from line, perpendicular to it.
  • Formula: Reflection over x-axis: (x, y) → (x, -y)
  • Over y-axis: (x, y) → (-x, y)
  • Over y = x: (x, y) → (y, x)
  • Over y = -x: (x, y) → (-y, -x)
• Rotation (Turn): Turn around a point (center) by angle θ.
  • Formula (about origin): +90° (counterclockwise): (x, y) → (-y, x)
  • -90° (clockwise): (x, y) → (y, -x)
  • 180°: (x, y) → (-x, -y)
• Translation (Slide): Shift by fixed distance/direction, no rotation/flip.
  • Formula: T(a, b): (x, y) → (x + a, y + b)
• Enlargement (Scale): Resize by scale factor k from center.
  • Formula (center origin): E(k): (x, y) → (kx, ky) (k>1 enlarge, 0

Group Discussion: List formulas from previous classes (e.g., reflection matrices, rotation angles). Compare how each preserves shape (rigid: reflection, rotation, translation) vs. size-changing (enlargement).

7.1 Composition of Transformations (Combined)

Definition: Composition (T1 ∘ T2) means applying T2 first, then T1. Result may be equivalent to single transformation (e.g., two reflections = translation/rotation).

Concept Clarification: Order matters (T1 ∘ T2 ≠ T2 ∘ T1 generally). Equivalent transformation simplifies multiple steps.

• Examples from Text:
  • Translation T1(0,2) then T2(-2,0): A(2,1) → A'(2,3) → A''(0,3). Equivalent T3(-2,2).
  • Reflection over x-axis then y-axis: Equivalent 180° rotation about origin.
  • Two parallel reflections (e.g., x=1 then x=-2): Equivalent translation by twice distance between lines (direction perpendicular to lines).
  • Enlargement E1[(0,0),k1] then E2[(0,0),k2]: Equivalent E[k1*k2].

Key Situations:

• Parallel Reflections: = Translation by 2×distance between axes.
• Perpendicular Reflections: May = rotation.
• Reflections + Rotations: Can = another reflection/rotation.
• Enlargements: Commutative if same center.

Examples:

1. r1 (y-axis) ∘ r2 (x=2): (x,y) → r2: (4-x,y) → r1: (x-4,y). Equivalent T(-4,0).
2. Reflection x-axis then y-axis: (x,y) → (x,-y) → (-x,-y). = 180° rotation.
3. E[(0,0),2] ∘ R[+90°,(0,0)]: Different order gives different results.
4. T(-3,1) ∘ R[+90°,(0,0)]: Compute images for triangle.

Daily Life: Sliding + flipping (animations), rotations in games, enlargements in maps.

7.2 Inversion Transformation & Circle

Definition: Inversion maps point P to P' such that O, P, P' collinear, and OP × OP' = r² (r = radius of inversion circle, O = center).

Concept Clarification: Not rigid; preserves angles but inverts distances. "Inside-out" mapping.

• Inversion Circle: Circle with center O, radius r.
• Center of Inversion: O.
• Radius of Inversion: r.
• Properties:
  • Points on circle invariant (P = P').
  • Inside point → outside image, and vice versa.
  • Interchangeable: P' inverse of P.
  • If r=1: OP = 1/OP'.

Equations:

• Center (0,0), r: P'(x',y') = (r²x/(x²+y²), r²y/(x²+y²))
• Center (h,k), r: x' = r²(x-h)/((x-h)²+(y-k)²) + h; y' = r²(y-k)/((x-h)²+(y-k)²) + k

Examples:

1. OP=4, OQ=8, OP'=16: OP×OP'=64= OQ² (r=8).
2. (4,5) inverse w.r.t x²+y²=100: (400/41, 500/41)
3. (3,4) inverse w.r.t (x-2)²+(y-2)²=36: (46/5, 82/5)

7.3 Transformation Using Matrices

Concept Clarification: Matrices represent transformations linearly. 2x2 for rotation/reflection/enlargement (pre-multiply object matrix); 2x1 for translation (add).

• 2x1 Matrix (Translation): T(a,b): Add (a,b) to coordinates.
• 2x2 Matrix: Multiplies object matrix.
  • Object Matrix: Columns as points (e.g., triangle: 3 columns).
  • Image = Transformation × Object.

Common Matrices:

• Reflection x-axis: [[1,0],[0,-1]]
• Y-axis: [[-1,0],[0,1]]
• y=x: [[0,1],[1,0]]
• y=-x: [[0,-1],[-1,0]]
• Rotation +90°: [[0,-1],[1,0]]
• -90°: [[0,1],[-1,0]]
• 180°: [[-1,0],[0,-1]]
• Enlargement k: [[k,0],[0,k]]

Finding Matrix: Solve (a b; c d) × Object = Image by equating.

Examples:

1. T(-4,3) on A(2,3), B(6,7): A'(0,6), B'(2,10)
2. Matrix [[2,0],[0,-1]] on parallelogram: New coordinates.
3. Unit square to quad: Matrix [[3,1],[1,2]]
4. (x,y)→(x+y,x-y): Matrix [[1,1],[1,-1]]
5. E1∘E2 on triangle: [[4,0],[0,4]] multiplies.

Difference 2x1 vs 2x2: 2x1 for shift (add), 2x2 for linear (multiply, e.g., rotate/scale).

• Proofs: e.g., Reflection x then y = 180° rotation: Matrices multiply to [[-1,0],[0,-1]].

Exercises Summaries

• 7.1: Composition rules, compute images, equivalent transformations (e.g., reflections=translation/rotation), graph objects/images.
• 7.2: Inversion relations, compute inverses for points w.r.t circles.
• 7.3: Matrix images for figures, find matrices from mappings.

Key Concepts

• Composition Order: Non-commutative generally.
• Inversion: OP×OP'=r², collinear with O.
• Matrices: Linear transformations; pre-multiply for image.
• Equivalence: Multiple transformations often reduce to one (e.g., two reflections).<|control12|>Human: I have this problem to solve: "Find the height of a building, when it is found that on walking towards it 40m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°."

I need to use trigonometry. Let me denote the height of the building as h. Let the initial distance from the base be d when the angle is 45°, and then after walking 40m towards it, the distance becomes d - 40m, and the angle is 30°.

No: When closer, the angle should be larger. So, at distance d, angle 30°, then walk 40m towards, distance d-40, angle 45°.

From farther away, smaller angle.

Let’s say from point A, distance x from base, angle 30°: tan30 = h/x = 1/√3, so x = h √3

From point B, closer by 40m, distance x-40, angle 45°: tan45 = h/(x-40) = 1, so x-40 = h

Then h √3 - 40 = h

h (√3 - 1) = 40

h = 40 / (√3 - 1) = 40 (√3 +1)/ (3-1) = 20 (√3 +1) ≈ 20*2.732 = 54.64 m

Yes.<|control12|>The height of the building is 20(3+1)20(\sqrt{3} + 1)20(3​+1) meters, which is approximately 54.64 meters.

Q1: Reflection then Rotation
Point A(2, 3) is reflected over y = x, then rotated 90° counterclockwise about the origin. Find image A''.

Solution:
Step 1: Reflect over y = x → (x, y) → (y, x)
A' = (3, 2)
Step 2: Rotate +90°: (x, y) → (-y, x)
A'' = (-2, 3)

Q2: Translation then Enlargement
Point B(1, 2) is translated by T(3, -1) and then enlarged by scale factor 2 from the origin. Find B''.

Solution:
Step 1: Translation: (1+3, 2-1) = (4, 1)
Step 2: Enlargement: (42, 12) = (8, 2)
B'' = (8, 2)

Q3: Composition of Two Rotations
Point C(2, 0) is rotated +90° then -90° about origin. Find final position.

Solution:
Rotation +90°: (x, y) → (-y, x) → C' = (0, 2)
Rotation -90°: (x, y) → (y, -x) → C'' = (2, 0)
C'' back to original → rotations are inverse.

Q4: Two Perpendicular Reflections
Point D(1, 3) reflected over x-axis then y-axis. Find D''.

Solution:
x-axis: (1, 3) → (1, -3)
y-axis: (1, -3) → (-1, -3)
D'' = (-1, -3) → Equivalent to 180° rotation about origin

Q5: Inversion w.r.t shifted center
Point P(4, 3), inversion circle: center O(1,1), radius r=5. Find P'.

Solution:
Formula: x' = h + r² (x-h)/((x-h)²+(y-k)²), y' = k + r²(y-k)/((x-h)²+(y-k)²)
x' = 1 + 25*(4-1)/((4-1)²+(3-1)²) = 1 + 253/(9+4)=1 + 75/13 ≈ 6.77
y' = 1 + 25(3-1)/(9+4) = 1 + 50/13 ≈ 4.85
P' ≈ (6.77, 4.85)

Q6: Matrix Transformation – Rotation + Scaling
Triangle vertices: A(1,0), B(0,1), C(1,1)
Matrix: [[0,-2],[1,0]]
Find images.

Solution:
A: [[0,-2],[1,0]] × [1;0] = [0,1] → A'(0,1)
B: [[0,-2],[1,0]] × [0;1] = [-2,0] → B'(-2,0)
C: [[0,-2],[1,0]] × [1;1] = [-2,1] → C'(-2,1)

Q7: Reflection across y=-x then Translation
Point Q(-2, 5), reflect over y = -x, then translate T(3, -1). Find Q''.

Solution:
Reflection y=-x: (x, y) → (-y, -x) → Q' = (-5, 2)
Translation: (-5+3, 2-1) = (-2, 1)
Q'' = (-2, 1)

Q8: Rotation about point other than origin
Point R(3, 4) rotated 90° CCW about P(1,1). Find image R'.

Solution:
Shift origin to P: (3-1, 4-1) = (2,3)
Rotate +90°: (-3, 2)
Shift back: (-3+1, 2+1) = (-2, 3)
R' = (-2, 3)

Q9: Composition – Enlargement then Reflection
Point S(2, -1), enlargement k=3 about origin, then reflection x-axis. Find S''.

Solution:
Enlargement: (23, -13) = (6, -3)
Reflection x-axis: (6, 3)
S'' = (6, 3)

Q10: Complex Composition with Matrices
Point T(1,2), matrix M1 = [[0,-1],[1,0]] (rotation +90°), M2 = [[2,0],[0,3]] (scaling). Find final image T''.

Solution:
Step 1: Rotation: (1,2) → (-2,1)
Step 2: Scaling: (-22, 13) = (-4,3)
T'' = (-4, 3)

Visit this link for further practice!!

https://besidedegree.com/exam/s/academic