1. Right-Angled Triangle

A triangle with one angle equal to 90° is called a right-angled triangle.
Let triangle ABC be right-angled at C.

Key Elements

Hypotenuse: Side opposite the right angle (longest side).

Perpendicular: Side opposite the angle θ.

Base: Side adjacent to angle θ.

Formulas

(a) Area of a Right-Angled Triangle
Area = 1/2 × base × height

(b) Pythagoras Theorem
(Hypotenuse)^2 = (Base)^2 + (Perpendicular)^2

(c) Trigonometric Ratios (for angle θ)
sin θ = Perpendicular / Hypotenuse
cos θ = Base / Hypotenuse
tan θ = Perpendicular / Base

(d) Common Values of Trigonometric Ratios

Example:
If AB = 6 cm, AC = 10 cm, find BC using Pythagoras theorem:

BC^2 + AB^2 = AC^2
BC^2 + 6^2 = 10^2
BC = 8 cm

Trigonometric ratios for ∠A:
sin A = BC / AC = 8 / 10 = 0.8
cos A = AB / AC = 6 / 10 = 0.6
tan A = BC / AB = 8 / 6 = 4 / 3

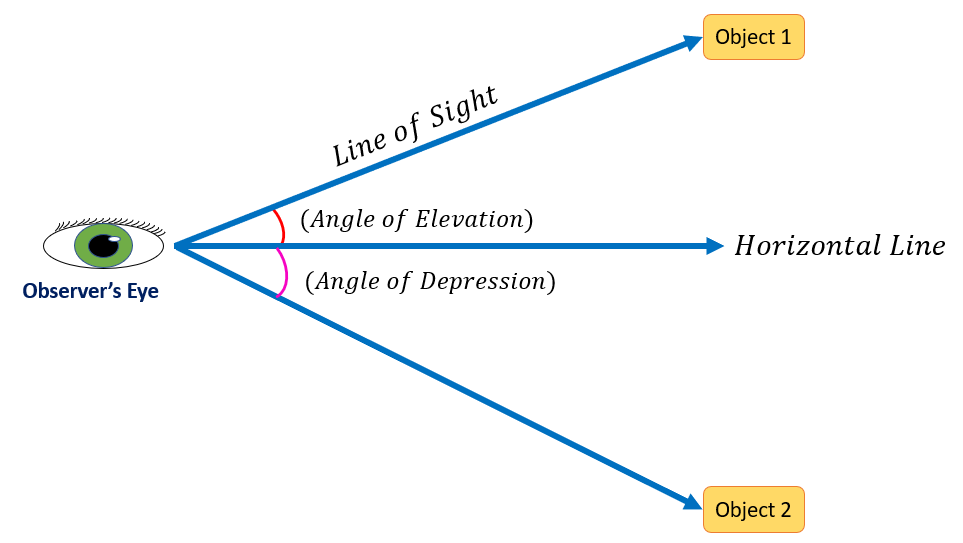
2. Angle of Elevation and Depression

Angle of Elevation: Angle formed by line of sight above horizontal when looking up at an object.

Angle of Depression: Angle formed by line of sight below horizontal when looking down.

Key Points:

Draw a line parallel to the ground from observer’s eye.

Angle of elevation = angle between line of sight and horizontal when looking up.

Angle of depression = angle between line of sight and horizontal when looking down.

Measured using a clinometer.

Observations:

Angle of elevation increases when object is closer.

Angle of depression increases when observer is closer to the object.

3. Applications of Trigonometry

Right-Triangle Relationships

tan θ = (Height of object − Observer height) / Distance from object
sin θ = (Height of object − Observer height) / Hypotenuse

4. Key Formulas for Solving Problems

Trigonometric ratios:
sin θ = Opposite / Hypotenuse
cos θ = Adjacent / Hypotenuse
tan θ = Opposite / Adjacent

Height of object:
Height = (tan θ × distance) + observer height

Distance of object:
Distance = (Height of object − observer height) / tan θ

Pythagoras theorem:
Hypotenuse^2 = Perpendicular^2 + Base^2

Angle from shadow:
tan θ = Height of object / Shadow length

5. Solved Examples (Basic & Important)

Example 1: Find height of tree
Angle of elevation = 45°, distance = 20 m, observer height = 1.8 m
tan 45° = (h − 1.8) / 20 ⇒ h = 21.8 m

Example 2: Distance to tower
Height = 140 m, angle = 60°
tan 60° = 140 / x ⇒ x = 80.83 m

Example 3: Broken tree
Height = 18 m, angle = 30°
sin 30° = (18 − x) / x ⇒ x = 12 m (broken part)

Example 4: Pole in circular pond
Height = 50 m, radius = 50 m
tan θ = 50 / 50 ⇒ θ = 45°

Example 5: Angle of depression to house
Tower height = 60 m, distance to house = 20 m, angle of depression = 45°
tan 45° = (60 − h) / 20 ⇒ h = 40 m (height of house)

Example 6: Two towers and distance between them
Two towers: 50 m and 30 m. Angles of elevation = 45° and 60°
tan 45° = 50 / x ⇒ x = 50 m
tan 60° = 30 / y ⇒ y = 30 / √3 ≈ 17.32 m

Example 7: Height of building using shadow
Shadow = 24 m, angle of elevation = 30°
tan 30° = h / 24 ⇒ h = 24 / √3 ≈ 13.86 m

Example 8: Observation tower problem
Observer height = 2 m, angles = 45° & 60°, walks 10 m closer
Let initial distance = x + 10
tan 45° = (h − 2) / (x + 10) ⇒ h − 2 = x + 10
tan 60° = (h − 2) / x ⇒ h − 2 = x√3
Solve: x ≈ 17.32 m, h ≈ 32 m

Example 9: Two points on opposite bank
Tree = 20 m, angles of elevation = 30° & 60°
tan 30° = 20 / x ⇒ x ≈ 34.64 m
tan 60° = 20 / y ⇒ y ≈ 11.55 m
Width of river = x + y ≈ 46.19 m

Example 10: Building on hill
Building = 50 m, hill = 30 m, angles = 60° & 45°
tan 45° = 30 / x ⇒ x = 30 m
tan 60° = 80 / x ⇒ x ≈ 46.19 m

Example 11: Ship approaching lighthouse
Lighthouse = 40 m, angles = 30° & 45°, ship sails 20 m closer
tan 30° = 40 / (x + 20) ⇒ x ≈ 49.28 m

Example 12: Pole leaning on another pole
Poles = 20 m & 15 m, distance = 10 m
tan θ = 5 / 10 ⇒ θ ≈ 26.57°

Example 13: Plane observation
Plane height = 500 m, angle = 30°
tan 30° = 500 / x ⇒ x ≈ 866.03 m

Example 14: Angle of depression from cliff
Cliff = 60 m, angles to boats = 30° & 45°
Distance to first boat = 60 / tan 30° ≈ 103.92 m
Distance to second boat = 60 / tan 45° = 60 m
Distance between boats ≈ 43.92 m

Example 15: Tree broken at top
Tree = 18 m, top touches ground 12 m from base
√(x^2 + 12^2) = 18 − x ⇒ x = 9 m (broken height)

Example 16: Two towers and observer
Towers = 60 m & 40 m, observer = 50 m from first, angle to second = 30°
tan 30° = 40 / (d − 50) ⇒ d ≈ 73.09 m

6. Important Notes for Exam

Remember trigonometric ratios for 0°, 30°, 45°, 60°, 90°.

Use Pythagoras theorem to find unknown sides.

Draw figure carefully; mark horizontal line for angles.

Closer object → larger angle of elevation; farther → smaller.

Convert height/distance problems into right triangles.

Practice Link:
https://besidedegree.com/exam/s/academic