Introduction to Circle
When we trace or stamp a two-rupee coin on paper, the figure formed is a circle.
A circle can also be drawn using a compass by fixing one leg at a point and rotating the other leg at a fixed distance.
A circle is defined as the locus of a point moving in a plane such that its distance from a fixed point always remains constant.
The fixed point is called the centre and the fixed distance is called the radius.
Parts of a Circle
Radius
A line segment joining the centre of a circle to any point on the circumference.
Circumference
The boundary of the circle.
Chord
A line segment joining any two points on the circumference.
Diameter
A chord passing through the centre of the circle.
It is the longest chord of the circle.
Arc
A part of the circumference of a circle.
Semi-circle
Half of a circle formed by a diameter.
Sector
The region enclosed by two radii and the arc between them.
Segment
The region enclosed by a chord and its corresponding arc.
Basic Observations about Circles
(a) There can be many circles with the same centre but different radii.
(b) A circle has infinitely many radii and diameters.
(c) Two circles having equal radii may or may not have the same centre.
(d) A diameter divides a circle into two equal semi-circles.
(e) The diameter is the longest chord of a circle.
(f) A straight line can intersect a circle at maximum two points.
Chord of a Circle
A chord is a line segment joining any two points on the circumference of a circle.
A diameter is a special chord that passes through the centre.
Theorem 1: A Perpendicular Drawn from the Centre of a Circle to a Chord Bisects the Chord
Statement
A perpendicular drawn from the centre of a circle to a chord bisects the chord.
Given
O is the centre of the circle.
AB is a chord of the circle.
OC ⟂ AB.
To Prove
AC = BC
Construction
Join OA and OB.[Fig1]
Proof
Statements||Reasons
∠OCA = ∠OCB | OC ⟂ AB, each angle is 90°
OA = OB | Radii of the same circle
OC = OC | Common side
ΔOAC ≅ ΔOBC | RHS congruence rule
AC = BC | Corresponding sides of congruent triangles
Hence proved.
Theorem 2: A Line Segment Joining the Centre of a Circle to the Midpoint of a Chord is Perpendicular to the Chord
Statement
A line segment joining the centre of a circle to the midpoint of a chord is perpendicular to the chord.
Given
P is the centre of the circle.
CD is a chord.
PM bisects CD.
To Prove
PM ⟂ CD
Construction
Join PC and PD.[FIG 2]
Proof
Statements |Reasons
PC = PD | Radii of the same circle
PM = PM | Common side
CM = DM | Given
ΔPMC ≅ ΔPMD | SSS congruence rule
∠PMC = ∠PMD | Corresponding angles
∠PMC + ∠PMD = 180° | Linear pair
2∠PMC = 180° | From step 5 and 6
∠PMC = 90° | Dividing both sides by 2
PM ⟂ CD | Definition of perpendicular
Hence proved.
Theorem 3: The Perpendicular Bisector of a Chord Passes Through the Centre of the Circle
Statement
The perpendicular bisector of a chord of a circle always passes through the centre.
Given
AB is a chord of a circle.
CD is the perpendicular bisector of AB.
To Prove
CD passes through the centre O.
Construction
Assume CD does not pass through O.
Join OD.[FIG 3]
Proof
Statements|| Reasons
CD ⟂ AB | Given
OD ⟂ AB | From Theorem 2
Two perpendiculars cannot be drawn from the same point to the same line | Geometrical fact
Assumption is wrong | Contradiction
CD passes through O | Hence proved
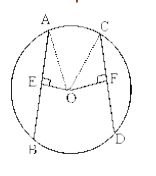
Theorem 4: Equal Chords of a Circle are Equidistant from the Centre
Statement
Equal chords of a circle are equidistant from the centre.
Given
O is the centre of the circle.
AB and CD are equal chords.
OE ⟂ AB and OF ⟂ CD.
To Prove
OE = OF
Construction
Join OA and OC.[FIG 4]
Proof
Statements||Reasons
∠OEA = ∠OFC | Each is 90°
OA = OC | Radii of the same circle
AE = CF | Halves of equal chords
ΔOEA ≅ ΔOFC | RHS congruence rule
OE = OF | Corresponding sides
Hence proved.
Theorem 5: Chords Equidistant from the Centre are Equal
Statement
Chords of a circle which are equidistant from the centre are equal.
Given
AB and CD are chords.
OE ⟂ AB and OF ⟂ CD.
OE = OF.
To Prove
AB = CD
Construction
Join OA and OC.[FIG 5]
Proof
Statements||Reasons
∠OEA = ∠OFC | Each equals 90°
OA = OC | Radii are equal
OE = OF | Given
ΔOEA ≅ ΔOFC | RHS congruence
AE = CF | Corresponding sides
AB = 2AE and CD = 2CF | Perpendicular bisects chord
AB = CD | Hence proved
Solved Examples
Example 1
Radius = 10 cm
Chord length = 16 cm
Solution
or, Let OM ⟂ AB
or, AM = ½ AB
or, AM = ½ × 16
or, AM = 8 cm
or, In ΔOMA
or, OA² = OM² + AM²
or, 10² = OM² + 8²
or, 100 = OM² + 64
or, OM² = 36
or, OM = 6 cm
Answer: Distance = 6 cm
Example 2
If ∠BAO = ∠CAO, prove AB = AC.
Solution
or, OA = OA (common side)
or, ∠BAO = ∠CAO (given)
or, Right angles at feet of perpendiculars
or, ΔOAF ≅ ΔOAE (SAA)
or, AF = AE
or, AB = AC
Example 3
A line intersects two concentric circles at A, B, C, D. Prove AB = CD.
Solution
or, Draw OM ⟂ AD
or, AM = DM
or, BM = CM
or, AB = AM − BM
or, CD = DM − CM
or, AB = CD
Important Questions (Exam-Type) with Solutions
Q1
Radius = 5 cm, distance of chord = 4 cm. Find length of chord.
Solution
or, OA = 5 cm
or, OM = 4 cm
or, OA² = OM² + AM²
or, 25 = 16 + AM²
or, AM² = 9
or, AM = 3
or, AB = 2 × AM
or, AB = 6 cm
Q2
Radius = 26 cm, chord = 48 cm. Find distance from centre.
Solution
or, AM = 24 cm
or, OA² = OM² + AM²
or, 676 = OM² + 576
or, OM² = 100
or, OM = 10 cm
Q3
Prove that a perpendicular drawn from the centre of a circle to a chord bisects the chord.
Proof
or, Let O be the centre and AB be the chord
or, Let OC ⟂ AB
or, Join OA and OB
or, In ΔOAC and ΔOBC
or, ∠OCA = ∠OCB = 90°
or, OA = OB (radii)
or, OC = OC (common side)
or, ΔOAC ≅ ΔOBC (RHS)
or, AC = BC
Hence proved.
Q4
Prove that equal chords of a circle are equidistant from the centre.
Proof
or, Let AB and CD be equal chords
or, Let OE ⟂ AB and OF ⟂ CD
or, Join OA and OC
or, In ΔOEA and ΔOFC
or, ∠OEA = ∠OFC = 90°
or, OA = OC (radii)
or, AE = CF (halves of equal chords)
or, ΔOEA ≅ ΔOFC (RHS)
or, OE = OF
Hence proved.
Q5
The radius of a circle is 26 cm and the length of a chord is 48 cm.
Find the distance of the chord from the centre.
Solution
or, Let O be the centre
or, Draw OM ⟂ AB
or, AM = ½ AB
or, AM = 24 cm
or, In ΔOMA
or, OA² = OM² + AM²
or, 26² = OM² + 24²
or, 676 = OM² + 576
or, OM² = 100
or, OM = 10 cm
Answer: Distance from centre = 10 cm
Q6
Prove that equal chords of a circle are equidistant from the centre.
Proof
or, Let AB and CD be equal chords
or, Let OE ⟂ AB and OF ⟂ CD
or, Join OA and OC
or, In ΔOEA and ΔOFC
or, ∠OEA = ∠OFC = 90°
or, OA = OC (radii)
or, AE = CF (halves of equal chords)
or, ΔOEA ≅ ΔOFC (RHS)
or, OE = OF
Hence proved..
Q7
Prove that chords equidistant from the centre of a circle are equal.
Proof
or, Let AB and CD be chords
or, OE ⟂ AB and OF ⟂ CD
or, OE = OF
or, Join OA and OC
or, In ΔOEA and ΔOFC
or, ∠OEA = ∠OFC = 90°
or, OA = OC
or, OE = OF
or, ΔOEA ≅ ΔOFC (RHS)
or, AE = CF
or, AB = 2AE
or, CD = 2CF
or, AB = CD
Hence proved.
Q8
If two chords are equal, what about their distances from centre?
Answer
They are equal.
Q9
If distances of two chords from centre are equal, what about chords?
Answer
They are equal.
Q10
Define segment of a circle.
Answer
The region enclosed by a chord and its arc.
For further practice visit this link !!
https://besidedegree.com/exam/s/academic
Gallery
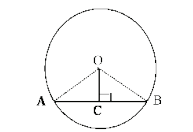
Fig 1
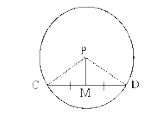
Fig 2
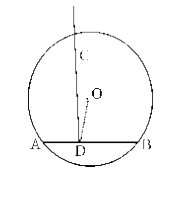
Fig 3
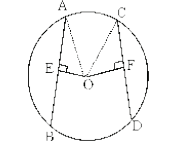
Fig 4