14.0 Review
A quadrilateral is a plane figure bounded by four line segments. In earlier classes, we studied different quadrilaterals such as square, rectangle, parallelogram, rhombus and trapezium along with their properties. In this chapter, we learn how to construct these quadrilaterals using ruler and compass based on given conditions.
14.1 Construction of Quadrilaterals
Construction in geometry means drawing figures accurately using only a ruler and a compass. Each step of construction must have a logical geometrical reason.
14.1.1 Construction of a Square
A square is a quadrilateral in which all sides are equal and each angle is 90°.
Case (a): To construct a square when one side is given
Steps:
Draw a line segment AB of given length.
Or, draw a perpendicular at A to AB.
Or, mark AD equal to AB on the perpendicular.
Or, draw a perpendicular at B to AB.
Or, mark BC equal to AB on this perpendicular.
Or, join C and D to obtain square ABCD.
Reason: Adjacent sides are perpendicular and all sides are equal. [fig1]
Case (b): To construct a square when diagonal is given
Steps:
Draw diagonal PR of given length.
Or, draw perpendicular bisector of PR meeting it at O.
Or, mark points Q and S on the bisector such that OQ = OS = half of PR.
Or, join PQ, QR, RS and SP.
Reason: Diagonals of a square bisect each other at right angles.[FIG :2]
14.1.2 Construction of a Rectangle
A rectangle is a parallelogram with one angle equal to 90°.
To construct a rectangle when one side and diagonal are given
Steps:
Draw side PQ of given length.
Or, draw a perpendicular at Q.
Or, with centre P and radius equal to diagonal, cut the perpendicular at R.
Or, with centres P and R and suitable radii, locate S.
Or, join PS and SR to complete rectangle PQRS.
Reason: A rectangle has right angles and equal diagonals. [FIG 3]
14.1.3 Construction of a Parallelogram
A parallelogram is a quadrilateral in which both pairs of opposite sides are parallel.
Case (a): Two adjacent sides and included angle are given
Steps:
Draw base PQ of given length.
Or, construct given angle at Q.
Or, mark QR on the angle arm.
Or, with centres P and R draw arcs to meet at S.
Or, join PS and RS to get parallelogram.
Reason: Opposite sides are equal and parallel.[FIG 4]
Case (b): Two adjacent sides and one diagonal are given
Steps:
Draw MN of given length.
Or, with centres M and N draw arcs to locate O.
Or, join NO.
Or, with centres M and O draw arcs to locate P.
Or, join MP and OP.
Reason: Diagonals and sides satisfy parallelogram properties. [FIG 5]
Case (c): One side and two diagonals are given
Steps:
Draw PQ of given length.
Or, draw arcs from P and Q to locate midpoint O of diagonals.
Or, extend PO and QO equally to get R and S.
Or, join PS, QR and RS.
Reason: Diagonals of a parallelogram bisect each other. [FIG 6]
Case (d): Two adjacent sides and height are given
Steps:
Draw base AB.
Or, draw perpendicular at B.
Or, mark height on perpendicular.
Or, draw line parallel to AB through height point.
Or, mark BC and AD on parallel line.
Or, join required sides. [FIG 7]
14.1.4 Construction of a Rhombus
A rhombus is a quadrilateral in which all sides are equal.
Case: One side and one diagonal are given
Steps:
Draw MN of given length.
Or, with centre M and radius of diagonal draw arc.
Or, with centre N and radius of side draw arc to meet at O.
Or, join MO and NO.
Or, with centres M and O draw arcs to locate P.
Or, join PM and PO.
Reason: All sides equal and diagonals bisect at right angles. [FIG 8]
14.1.5 Construction of a Trapezium
A trapezium is a quadrilateral with one pair of opposite sides parallel.
To construct trapezium when three sides and one angle are given
Steps:
Draw base AB.
Or, construct given angle at B.
Or, mark BC on angle arm.
Or, construct supplementary angle at C.
Or, mark CD on this ray.
Or, join AD to get trapezium.
Reason: One pair of opposite sides is parallel. [FIG 9]
Important Questions with Solutions
Construct a square of side 6 cm.
Solution:
Draw AB = 6 cm.
Or, draw perpendiculars at A and B.
Or, mark AD = BC = 6 cm.
Or, join CD.
Hence, ABCD is the required square.
Construct a rectangle with one side 5 cm and diagonal 7 cm.
Solution:
Draw PQ = 5 cm.
Or, draw perpendicular at Q.
Or, cut arc of radius 7 cm from P.
Or, complete rectangle.
Hence, required rectangle is obtained.
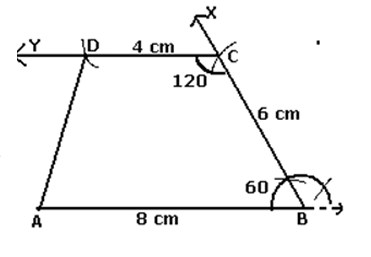
Construct a parallelogram with sides 6 cm, 4 cm and angle 120°.
Solution:
Draw PQ = 6 cm.
Or, construct angle 120° at Q.
Or, mark QR = 4 cm.
Or, complete parallelogram.
Construct a parallelogram when one side and two diagonals are given.
Solution:
Draw base.
Or, locate midpoint of diagonals.
Or, extend equally.
Or, join vertices.
Construct a rhombus when side = 5 cm and diagonal = 8 cm.
Solution:
Draw side.
Or, draw arcs.
Or, locate remaining vertices.
Construct a trapezium with one pair of parallel sides.
Solution:
Draw base.
Or, construct angles.
Or, mark sides.
Explain why diagonals of a square bisect at right angles.
Solution:
Diagonals of a square are equal.
Or, they bisect each other.
Or, they intersect at 90°.
Can a quadrilateral be constructed with sides 3,4,5,6 cm?
Solution:
Yes, if sum of any three sides is greater than the fourth.
Or, construction is possible.
Is converse of 'diagonals of rhombus bisect each other' true?
Solution:
Yes, diagonals bisecting at right angle imply rhombus.
Why is a rectangle a parallelogram?
Solution:
Opposite sides are equal.
Or, opposite sides are parallel.
For further practice visit this link !!
https://besidedegree.com/exam/s/academic
Gallery
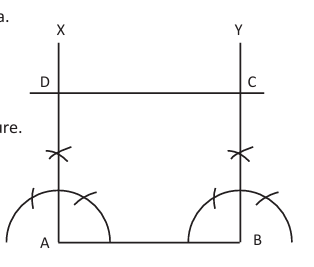
Fig 1
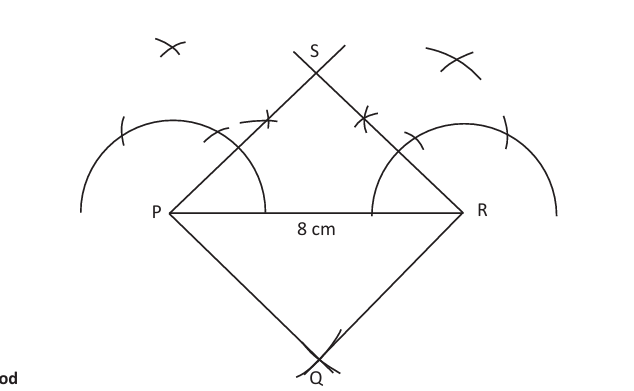
Fig 2
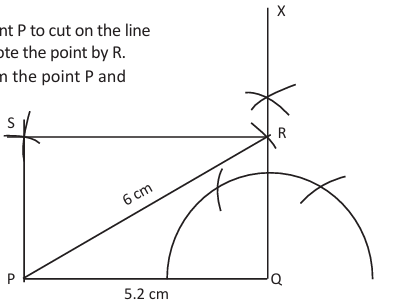
Fig 3
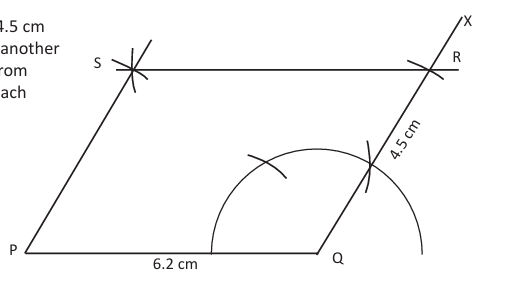
Fig 4
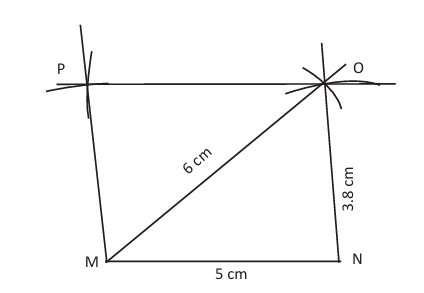
Fig 5
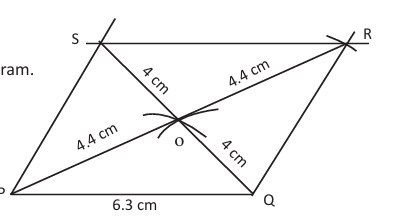
Fig 6
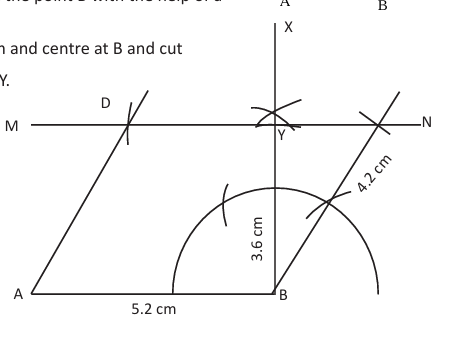
Fig 7
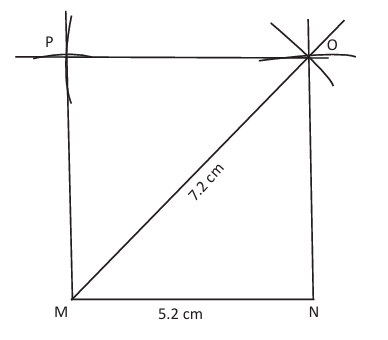
Fig 8