INTRODUCTION
A quadrilateral whose opposite sides are parallel is called a parallelogram. Using this definition and basic geometrical facts, we can study and prove different properties of a parallelogram. These properties are very useful in solving geometrical problems and are also extended to triangles using mid-point theorems.
DEFINITION OF PARALLELOGRAM
A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.
BASIC PROPERTIES OF A PARALLELOGRAM
Opposite sides are equal
Opposite angles are equal
Diagonals bisect each other
Consecutive angles are supplementary (sum is 180°)
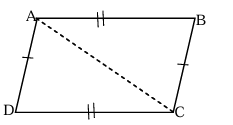
THEOREM 1 : OPPOSITE SIDES AND OPPOSITE ANGLES OF A PARALLELOGRAM ARE EQUAL
Given
ABCD is a parallelogram such that AB // CD and AD // BC
To Prove
AB = CD and AD = BC
∠ABC = ∠ADC and ∠DAB = ∠BCD
Construction
Join BD [FIG 1]
Proof
Statements
In ΔABD and ΔBDC
i. ∠ABD = ∠BDC
ii. BD = BD
iii. ∠ADB = ∠CBD
ΔABD ≅ ΔBDC
AB = CD and AD = BC
∠DAB = ∠BCD
∠ABD + ∠DBC = ∠BDC + ∠ADB
∠ABC = ∠ADC
Reasons
Alternate angles, Common side, Alternate angles
ASA congruence axiom
Corresponding sides of congruent triangles
Corresponding angles of congruent triangles
Adding equal angles to equal angles
From statement 5
Hence, opposite sides and opposite angles of a parallelogram are equal. Proved.
THEOREM 2 : QUADRILATERAL WHOSE OPPOSITE SIDES ARE EQUAL IS A PARALLELOGRAM
Given
ABCD is a quadrilateral such that AB = CD and AD = BC
To Prove
AB // CD and AD // BC
Construction
Join AC[fig2]
Proof
Statements
In ΔABC and ΔACD
i. AB = CD
ii. AD = BC
iii. AC = AC
ΔABC ≅ ΔACD
∠ACB = ∠DAC and ∠BAC = ∠ACD
AB // CD and AD // BC
ABCD is a parallelogram
Reasons
Given, Given, Common side
SSS congruence axiom
Corresponding angles
Alternate angles
Opposite sides are parallel
Hence, ABCD is a parallelogram. Proved.
THEOREM 3 : QUADRILATERAL WHOSE OPPOSITE ANGLES ARE EQUAL IS A PARALLELOGRAM
Given
∠ABC = ∠ADC and ∠DAB = ∠BCD
To Prove
AB // CD and AD // BC
Proof
Statements
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
∠ABC + ∠BCD + ∠ABC + ∠BCD = 360°
Or, 2∠ABC + 2∠BCD = 360°
Or, ∠ABC + ∠BCD = 180°
AB // CD
∠BCD + ∠CDA = 180°
AD // BC
ABCD is a parallelogram
Reasons
Sum of angles of a quadrilateral
Given opposite angles are equal
Consecutive interior angles
Angle sum property
Consecutive interior angles
Opposite sides are parallel
Hence, ABCD is a parallelogram. Proved.
THEOREM 4 : JOINING END POINTS OF EQUAL AND PARALLEL LINE SEGMENTS
Statement
Two line segments joining the end points of two equal and parallel line segments towards the same side are also equal and parallel.
Given
AB = CD and AB // CD
To Prove
AC = BD and AC // BD
Construction
Join BC [Fig4]
Proof
Statements
In ΔABC and ΔBCD
i. AB = CD
ii. ∠ABC = ∠BCD
iii. BC = BC
ΔABC ≅ ΔBCD
AC = BD
∠ACB = ∠CBD
AC // BD
Reasons
Given, Alternate angles, Common side
SAS congruence axiom
Corresponding sides
Corresponding angles
Alternate angles
Hence, AC = BD and AC // BD. Proved.
THEOREM 5 : JOINING OPPOSITE END POINTS OF EQUAL AND PARALLEL LINE SEGMENTS
Statement
Two line segments joining the opposite end points of two equal and parallel line segments bisect each other.
Given
PQ = RS and PQ // RS, PS and QR meet at O
To Prove
PO = OS and QO = OR
Proof
Statements
In ΔPOQ and ΔROS
i. ∠OPQ = ∠OSR
ii. PQ = RS
iii. ∠PQO = ∠SRO
ΔPOQ ≅ ΔROS
PO = OS and QO = OR
PS and QR bisect each other
[Fig5]
Reasons
Alternate angles, Given, Alternate angles
ASA congruence axiom
Corresponding sides
Definition of bisection
Hence, PS and QR bisect each other. Proved.
THEOREM 6 : DIAGONALS OF A PARALLELOGRAM BISECT EACH OTHER
Given
PQRS is a parallelogram. Diagonals PR and QS intersect at O
To Prove
PO = OR and QO = OS
[Fig6]
Proof
Statements
In ΔPOQ and ΔROS
i. ∠OPQ = ∠ORS
ii. PQ = RS
iii. ∠OQP = ∠OSR
ΔPOQ ≅ ΔROS
PO = OR and QO = OS
PR and QS bisect each other
Reasons
Alternate angles, Opposite sides, Alternate angles
ASA congruence axiom
Corresponding sides
From statement 3
Hence, diagonals of a parallelogram bisect each other. Proved.
THEOREM 7 : QUADRILATERAL WHOSE DIAGONALS BISECT EACH OTHER IS A PARALLELOGRAM
Given
Diagonals AC and BD of quadrilateral ABCD bisect each other at O
To Prove
ABCD is a parallelogram
[Fig7]
Proof
Statements
In ΔAOB and ΔCOD
i. AO = OC
ii. ∠AOB = ∠COD
iii. OB = OD
ΔAOB ≅ ΔCOD
AB = DC
∠OBA = ∠ODC
AB // DC
ABCD is a parallelogram
Reasons
Given, Vertically opposite angles, Given
SAS congruence axiom
Corresponding sides
Corresponding angles
Alternate angles
Opposite sides equal and parallel
Hence, ABCD is a parallelogram. Proved.
MID-POINTS OF A TRIANGLE
The properties of parallelogram help us understand relations between mid-points of sides of a triangle.
THEOREM 8 : LINE THROUGH MID-POINT PARALLEL TO ONE SIDE OF A TRIANGLE
Given
In ΔABC, E is the mid-point of AB (AE = EB) and EF // BC
To Prove
AF = FC
Construction
Draw FD // EB meeting BC at D [Fig8]
Proof
Statements
EFDB is a parallelogram
EB = FD
AE = EB
AE = FD
ΔAEF ≅ ΔCFD
AF = FC
Reasons
Opposite sides parallel
Opposite sides of parallelogram
Given
From 2 and 3
SAA congruence axiom
Corresponding sides
Hence, the third side is bisected. Proved.
THEOREM 9 : LINE JOINING MID-POINTS OF TWO SIDES OF A TRIANGLE
Given
In ΔABC, E and F are mid-points of AB and AC
To Prove
EF // BC
Construction
Produce EF to D such that FD = EF and join CD [Fig9]
Proof
Statements
ΔAEF ≅ ΔDFC
∠AEF = ∠CDF
BE // CD
BCDE is a parallelogram
EF // BC
Reasons
SAS congruence axiom
Corresponding angles
Alternate angles
Opposite sides equal and parallel
Opposite sides of parallelogram
Hence, EF is parallel to BC. Proved.
IMPORTANT QUESTIONS WITH SOLUTIONS
QUESTION 1
If one angle of a parallelogram is 90°, prove all angles are 90°.
Solution:
∠ABC = 90°
Or, ∠BAD + ∠ABC = 180°
Or, ∠BAD + 90° = 180°
Or, ∠BAD = 90°
Or, opposite angles of a parallelogram are equal
Or, ∠BCD = 90° and ∠ADC = 90°
Hence all angles are 90°
Proved.
QUESTION 2
Find x if consecutive angles are (3x – 20)° and (2x + 10)°.
Solution:
(3x – 20) + (2x + 10) = 180
Or, 5x – 10 = 180
Or, 5x = 190
Or, x = 38
Answer: x = 38
QUESTION 3
Diagonals of ABCD bisect each other. Prove it is a parallelogram.
Solution:
AO = OC and BO = OD
Or, triangles AOB and COD are congruent
Or, opposite sides become equal and parallel
Or, ABCD is a parallelogram
Proved.
QUESTION 4
In ΔABC, D and E are mid-points of AB and AC. Find DE if BC = 6 cm.
Solution:
DE = ½ BC
Or, DE = ½ × 6
Or, DE = 3 cm
Answer: DE = 3 cm
QUESTION 5
If opposite sides of a quadrilateral are equal, prove it is a parallelogram.
Solution:
AB = CD and AD = BC
Or, triangles formed are congruent
Or, corresponding angles are equal
Or, opposite sides are parallel
Hence it is a parallelogram
Proved.
QUESTION 6
In a rhombus, one angle is 60°. Find all angles.
Solution:
Opposite angles are equal
Or, two angles = 60°
Or, adjacent angles = 180 – 60
Or, adjacent angles = 120°
Hence angles are 60°, 120°, 60°, 120°
QUESTION 7
If diagonals of a quadrilateral bisect at right angles, name the figure.
Solution:
Diagonals bisect each other
Or, diagonals intersect at 90°
Or, figure is a rhombus
Answer: Rhombus
QUESTION 8
If mid-points of a quadrilateral are joined, what is formed?
Solution:
Opposite sides become equal and parallel
Or, figure formed is a parallelogram
Answer: Parallelogram
QUESTION 9
Find x if opposite angles are (4x – 10)° and (2x + 30)°.
Solution:
4x – 10 = 2x + 30
Or, 4x – 2x = 40
Or, 2x = 40
Or, x = 20
Answer: x = 20
QUESTION 10
If diagonals of a parallelogram are equal, name the figure.
Solution:
Diagonals bisect each other
Or, diagonals are equal
Or, figure is a rectangle
Answer: Rectangle
For further practice visit this link !!
https://besidedegree.com/exam/s/academic
Gallery
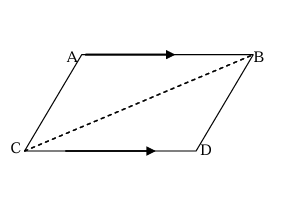
Fig 4
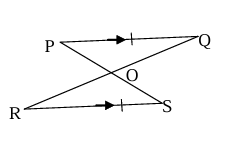
Fig 5
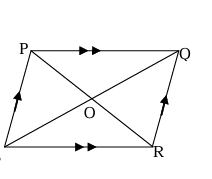
Fig 6
Fig 7
Fig 8
Fig 9
Fig 1