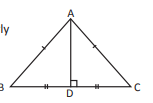
Definition of a Triangle
A closed plane figure bounded by three line segments is called a triangle.
Classification of Triangles on the Basis of Sides
i. Scalene Triangle: A triangle having unequal sides is called a scalene triangle.
ii. Isosceles Triangle: A triangle having two sides equal is called an isosceles triangle.
iii. Equilateral Triangle: A triangle having all sides equal is called an equilateral triangle.
Classification of Triangles on the Basis of Angles
i. Acute-Angled Triangle: A triangle having all angles less than 90° is called an acute-angled triangle.
ii. Obtuse-Angled Triangle: A triangle having one angle greater than 90° is called an obtuse-angled triangle.
iii. Right-Angled Triangle: A triangle having one angle exactly 90° is called a right-angled triangle.
Verification of Geometrical Properties
Properties of a triangle include angle relationships, side relationships, and angle-side relationships. For example: sum of internal angles is 180°, sum of two sides greater than third.
Experimental verification (inductive approach): Draw figures, measure, and conclude based on observations.
Theoretical proof (deductive approach): Use definitions, axioms, postulates, and logical steps without measurement.
Discussion: In previous classes, we used both; now focus on deductive proofs.
Angle Relation on Parallel Lines
Draw at least three horizontal parallel lines using ruler and set square. Intersect with at least three oblique parallel lines. Observe formed figures and angles: alternate angles equal, corresponding angles equal, interior angles supplementary.
In triangle ABC with parallel lines, find relations.
For figure: Parallel lines intersected, triangle ABC with angles 1,2,3.
Questions:
(a) Alternate angles of ∠1 and ∠2.
(b) ∠ACB + ∠ABC + ∠BAC = ∠1 + ∠2 + ∠3 (because of alternate and corresponding angles).
(c) ∠1 + ∠2 + ∠3 = 180° (straight line).
(d) Sum of internal angles of triangle ABC is 180°.
(e) Draw other triangles and verify.
This uses parallel lines to prove sum of angles in triangle is 180°.
Theorem 1: The Sum of Internal Angles of a Triangle is Equal to 180°
Given: Triangle ABC with angles ∠BAC, ∠ABC, ∠ACB.
To prove: ∠BAC + ∠ABC + ∠ACB = 180°.
Construction: Produce BC to E, draw CD parallel to BA.
Proof:
- ∠BAC = ∠ACD (alternate angles, BA || CD).
- ∠ABC = ∠DCE (corresponding angles, BA || CD).
- ∠BCA + ∠ACD + ∠DCE = 180° (straight line at C on BE).
- ∠BCA + ∠BAC + ∠ABC = 180° (substitute 1 and 2 into 3).
Figure description: Triangle ABC, BC extended to E, CD parallel to BA, point D on extension.[FIG:1]
Theorem 2: The Exterior Angle of a Triangle is Equal to the Sum of Two Opposite Interior Angles
Given: Triangle ABC, BC produced to D, ∠ACD exterior, ∠ABC and ∠BAC opposite interior.
To prove: ∠ACD = ∠ABC + ∠BAC.
Proof:
- ∠ABC + ∠ACB + ∠BAC = 180° (Theorem 1).
- ∠ACB + ∠ACD = 180° (linear pair).
- ∠ABC + ∠ACB + ∠BAC = ∠ACB + ∠ACD (from 1 and 2).
- ∠ABC + ∠BAC = ∠ACD (subtract ∠ACB).
Figure description: Triangle ABC, BC extended to D, exterior angle at C.[FIG:2]
Example 1
In figure, BE ⊥ AC, ∠EBC=30°, ∠DAC=20°. Find ∠ACD, ∠ADB, ∠AMB.
Solution:
BE ⊥ AC, so ∠BEC=90°.
In triangle BEC: ∠BEC + ∠EBC + ∠ECB = 180°.
Or, 90° + 30° + ∠ECB = 180°.
Or, ∠ECB = 60° (but ∠ECB is ∠ACD).
So, ∠ACD=60°.
∠ADB = ∠DAC + ∠ACD (Theorem 2) =20°+60°=80°.
∠AMB = ∠MBD + ∠BDM (in triangle BMD, but assuming points) =30°+80°=110°.
Figure description: Points A,B,C,D,M,E with BE perp AC.
Example 2
BC produced to D, ∠ABC and ∠ACD bisected by BE and CE. Prove ∠BAC=2∠BEC.
Solution:
∠ABC=2∠EBC, ∠ACD=2∠ECD (bisectors).
∠BAC + ∠ABC = ∠ACD (Theorem 2).
Or, ∠BAC = ∠ACD - ∠ABC =2∠ECD - 2∠EBC=2(∠ECD - ∠EBC).
In triangle EBC: ∠EBC + ∠BEC = ∠ECD (Theorem 2).
Or, ∠BEC=∠ECD - ∠EBC.
Thus, ∠BAC=2∠BEC.
Figure description: Triangle ABC, extended to D, bisectors BE,CE.
Exercise 12.1 (Summary)
- Find x,y,z in figures (various triangles with angles).
- Sum of interior angles in polygons by dividing into triangles.
- BO,CO bisectors, ∠BAC=60°, prove ∠BOC=120°.
- BC produced both sides, prove ∠ABE + ∠ACD + ∠BAC=180°.
- Exterior angles: 6 formed (each side both ways), sum 360°, relation: each exterior=180°-interior.
- Parallels through vertices, prove sum 180°.
Properties of Isosceles Triangle
Isosceles: two equal sides, symmetric.
Base angles equal.
Uses congruent triangles.
Conditions for Congruency of Triangles
SSS, SAS, ASA, AAS, RHS (right angle, hypotenuse, side).
Not SSA generally.
Verify with compass/ruler.
Theorem 3: The Base Angles of an Isosceles Triangle are Equal
Given: ABC isosceles, AB=AC.
To prove: ∠ABC=∠ACB.
Construction: Bisect ∠BAC by AD.
Proof:
In ABD, ACD: AB=AC (S), ∠BAD=∠CAD (A), AD common (S).
SAS congruent.
∠ABD=∠ACD (corresponding).
Figure: Triangle ABC, AD to base BC.[FIG:3]
Theorem 4: Converse of Theorem 3
If two angles equal, opposite sides equal.
Given: ∠ABC=∠ACB.
Prove: AB=AC.
Construction: Bisect ∠BAC by AD.
Proof: Angles equal (A), bisected (A), common AD (S). AAS congruent. Sides equal.[FIG:4]
Theorem 5: The Bisector of the Vertical Angle of an Isosceles Triangle Bisects the Opposite Side Perpendicularly
Given: AB=AC, AD bisects ∠BAC.
Prove: BD=DC, AD perp BC.
Proof: SAS congruent as above, then BD=DC, ∠BDA=∠CDA, sum 180°, each 90°.[FIG:5]
Theorem 6: Converse of Theorem 5
Given: AB=AC, AD bisects BC perp.
Prove: ∠BAD=∠CAD.
Proof: RHS congruent (right, hypotenuse AB=AC, side BD=DC). Angles equal.[FIG:6]
Example 3
(a) AB=AC, ∠BAC=50°, find x (base angles).
Solution: Base angles equal, x each.
2x+50=180, 2x=130, x=65.
(b) ∠ABC=6x, ∠BAC=3x, AB=AC.
Base equal, so ∠ACB=6x.
6x+6x+3x=180, 15x=180, x=12.
Example 4
(a) ∠ABC=∠ACB=50°, AC=4cm, AB=x.
Opposite equal angles, AB=AC=4, x=4.
(b) AB=AC, AD perp BC, DC=x, BD=3.
Bisects, BD=DC, x=3.
Example 5
PQ=PR, AQ=BR. Prove AP=BP, ∠PAB=∠PBA.
Proof: In APQ, BRP: PQ=PR (S), base angles equal (A), QA=BR (S). SAS congruent. AP=BP. Then isosceles APB, base angles equal.
Figure: Triangle PQR isosceles, A on PQ, B on PR.
Exercise 12.2 (Summary)
- Find x in isosceles figures.
- Find x,y,z in figures.
- (a) AB=AC, PQ||BC, prove AP=AQ.
(b) AO=OB=OC, prove ∠BAC=90°.
(c) ABC, BCD isosceles, prove ∠ABD=∠ACD.
- Prove equilateral angles equal, converse.
- Equilateral is isosceles? Yes, all sides equal includes two equal.
- List objects with isosceles: roof, bridge, etc.
Pythagoras Theorem
In right-angled triangle, hypotenuse² = base² + perpendicular².
Discuss: Increasing angle lengthens opposite side; short paths; graph verification; if not inequality, no triangle.
Example 1
∠BAC=50°, ∠ABC=60°. Find largest/smallest sides.
∠ACB=70° (largest), so AB longest; ∠BAC smallest, BC shortest.
Example 2
AB=AC=25cm, BC=14cm, AD perp BC. Find AD.
BD=DC=7cm.
25² = AD² +7², 625=AD²+49, AD²=576, AD=24cm.
Example 3
AB=BC, relation AD,CD.
AB=BC so ∠BAC=∠BCA.
∠DAC < ∠BAC so < ∠BCA, thus DC < AD.
Important Questions
Q1.
In a triangle, two angles are 40° and 60°. Find the measure of the third angle.
Solution:
The sum of interior angles of a triangle is 180°.
Or, third angle + 40° + 60° = 180°
Or, third angle + 100° = 180°
Or, third angle = 180° – 100°
∴ Third angle = 80°
(Explanation: This is the basic application of Theorem 1 – sum of angles in a triangle is 180°.)
Q2.
Find the sum of the interior angles of a quadrilateral.
Solution:
A quadrilateral can be divided into 2 triangles by drawing one diagonal.
Each triangle has angle sum 180°.
Or, total sum = 180° + 180° = 360°
(Alternative formula: Sum of interior angles of polygon = (n–2) × 180°, where n = 4
∴ (4–2) × 180° = 360°)
Q3.
In △ABC, BO and CO are the bisectors of ∠ABC and ∠ACB respectively. Given that ∠BAC = 60°, prove that ∠BOC = 120°.
Solution:
Let ∠ABC = ∠ACB = y (we will find actual value).
In △ABC:
∠BAC + ∠ABC + ∠ACB = 180°
60° + y + y = 180°
60° + 2y = 180°
2y = 120°
y = 60°
So △ABC is equilateral (all angles 60°).
Since BO and CO are angle bisectors:
∠OBC = ∠OBA = 30°
∠OCB = ∠OCA = 30°
Now in △BOC:
∠BOC + ∠OBC + ∠OCB = 180°
∠BOC + 30° + 30° = 180°
∠BOC + 60° = 180°
∠BOC = 120°
Q4.
In isosceles triangle ABC with AB = AC, the vertex angle ∠BAC = 40°. Find the measure of each base angle.
Solution:
In isosceles triangle, base angles are equal (Theorem 3).
Let each base angle = x
Then:
x + x + 40° = 180°
2x + 40° = 180°
2x = 140°
x = 70°
∴ Each base angle is 70°.
Q5.
In △ABC, AB = AC and PQ ∥ BC (P on AB, Q on AC). Prove that AP = AQ.
Solution:
Given: AB = AC (isosceles triangle) and PQ ∥ BC.
Since PQ ∥ BC:
∠APQ = ∠ABC (corresponding angles)
∠AQP = ∠ACB (corresponding angles)
But ∠ABC = ∠ACB (base angles of isosceles △ABC)
∴ ∠APQ = ∠AQP
Therefore, in △APQ, two base angles are equal
∴ △APQ is isosceles
∴ sides opposite equal angles are equal
∴ AP = AQ (proved)
Q6.
In △ABC, ∠A = 90°, ∠B = 50°, ∠C = 40°. Identify the longest side, shortest side, largest angle and smallest angle.
Solution:
Largest angle = ∠A = 90° (opposite side BC) → BC is the longest side
Smallest angle = ∠C = 40° (opposite side AB) → AB is the shortest side
(Explanation: In any triangle, larger angle is opposite longer side and vice versa.)
Q7.
In right-angled triangle ABC with right angle at A, AB = 9 cm, AC = 40 cm. Find the length of hypotenuse BC.
Solution:
By Pythagoras theorem:
BC² = AB² + AC²
BC² = 9² + 40²
BC² = 81 + 1600
BC² = 1681
BC = √1681
BC = 41 cm
Q8.
Prove that a triangle with sides m² – n², 2mn and m² + n² (where m > n > 0) is a right-angled triangle.
Solution:
Let:
a = m² – n²
b = 2mn
c = m² + n² (hypotenuse candidate)
Check Pythagoras: a² + b² ? = c²
a² + b² = (m² – n²)² + (2mn)²
= m⁴ – 2m²n² + n⁴ + 4m²n²
= m⁴ + 2m²n² + n⁴
= (m² + n²)²
= c²
Since a² + b² = c², the triangle is right-angled at the vertex between sides a and b.
Q9.
Find the length of the altitude (height) drawn from the vertex to the base in an equilateral triangle with side 10 cm.
Solution:
In equilateral triangle, altitude also bisects the base.
Base = 10 cm → each half = 5 cm
By Pythagoras theorem in right triangle formed:
h² + 5² = 10²
h² + 25 = 100
h² = 75
h = √75
h = 5√3 cm
(Exact answer: 5√3 cm ≈ 8.66 cm)
Q10.
In rectangle ABCD, diagonal AC = 20 cm and side AB = 16 cm. Find the lengths of diagonal BD and side AD.
Solution:
In rectangle, diagonals are equal → BD = AC = 20 cm
In right-angled △ABC (right angle at B):
AC² = AB² + BC²
20² = 16² + AD² (since BC = AD)
400 = 256 + AD²
AD² = 144
AD = √144
AD = 12 cm
For further practice visit this link !!
https://besidedegree.com/exam/s/academic
Gallery
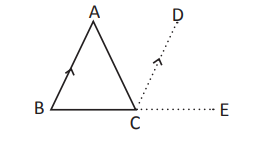
Fig 1
Fig 2
Fig 3
Fig 4
Fig 5