1.1 Function
A function is a relation where each element in the domain corresponds to exactly one element in the range.
Examples of functions:
Each person → annual income
Each square → area
Each number → its cube
1.1.0 Review: Square Example
Given a square with side length lll:
Area function:
- f(l)=l2f(l) = l^2f(l)=l2
Perimeter function:
- g(l)=4lg(l) = 4lg(l)=4l
Are the functions one-to-one?
f(l) = l²: Not one-to-one if domain includes negative numbers.
g(l) = 4l: One-to-one.
Are the functions onto?
f(l) = l²: Not onto if range includes negative numbers.
g(l) = 4l: Onto for all real numbers.

1.1.1 Algebraic Functions
An algebraic function is a function formed using algebraic expressions with variables.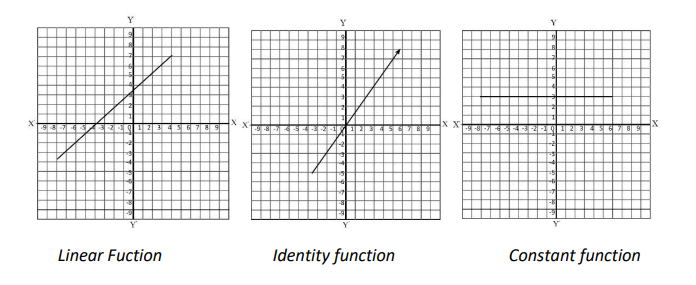
Types of Algebraic Functions
1. Linear function:
f(x) = mx + c
Example:
f(x) = 2x + 3
Special cases:
m = 0 → Constant function: f(x) = c
m = 1, c = 0 → Identity function: f(x) = x
2. Quadratic function:
f(x) = ax² + bx + c, a ≠ 0
Graph: Parabola
Vertex form: f(x) = a(x − h)² + k → Vertex at (h, k)
Example:
f(x) = x² + 2x + 2
= (x + 1)² + 1
Vertex: (-1, 1)
3. Cubic function:
f(x) = ax³ + bx² + cx + d, a ≠ 0
Graph passes through origin if b = c = d = 0
Can have up to 3 real roots
Basic Exercises (Solved)
Linear function:
f(x) = x + 2
Graph: Straight line passing through (0, 2) with slope 1
Quadratic function:
y = -x²
Graph: Parabola opening downward
Cubic function:
y = x³
Graph: S-shaped curve passing through origin
1.1.1 (b) Trigonometric Functions
Functions: sin x, cos x, tan x
Periods:
sin x, cos x → 2π
tan x → π
Graph properties:
sin x, cos x → values between -1 and 1
tan x → vertical asymptotes at odd multiples of π/2
Example:
y = 2 sin x → amplitude 2, period 2π
1.1.2 Composition of Functions
Definition: Combining two functions f and g such that output of one becomes input of another.
(g ∘ f)(x) = g(f(x))
(f ∘ g)(x) = f(g(x))
Example:
f(x) = 3 + 2x
g(x) = x² + 1
Step 1: g(f(x)) = (3 + 2x)² + 1
Step 2: Expand → 9 + 12x + 4x² + 1
Step 3: Simplify → 4x² + 12x + 10
Note: Composition exists only if range of first function is subset of domain of second function.
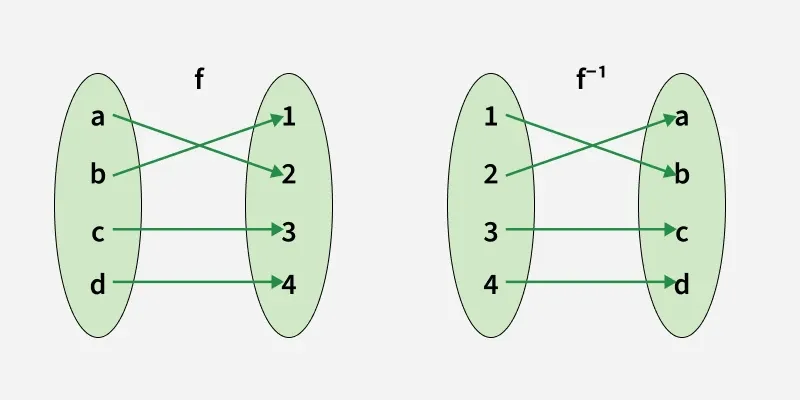
1.1.3 Inverse of Functions
Definition: If f is one-to-one and onto, there exists f⁻¹ such that:
f(x) = y ⟺ f⁻¹(y) = x
Steps to find inverse:
Replace f(x) with y → y = f(x)
Swap x and y → x = f(y)
Solve for y → y = f⁻¹(x)
Example:
f(x) = 2x + 3
Step 1: y = 2x + 3
Step 2: x = 2y + 3
Step 3: y = (x − 3) / 2
f⁻¹(x) = (x − 3) / 2
Property:
(f⁻¹ ∘ f)(x) = (f ∘ f⁻¹)(x) = x
1.1.4 Functional Relations in Real Life
Square → Area
Height → Ideal weight
Paddy → Rice → Flour (composition)
1.1.5 Miscellaneous
Volume of Sphere: V = 4/3 × π × r³
Surface Area of Sphere: A = 4 × π × r²
Functional relation:
V(r) = 4/3 × π × r³, A(r) = 4 × π × r²
Inverse functions: Solve for r in terms of V or A.
Common Questions Solved
Linear function:
y = 3x + 2
Vertex of y = x² + 4x + 3:
h = −b / 2a = −4 / 2 = −2
k = f(−2) = (−2)² + 4(−2) + 3 = −1
Vertex: (−2, −1)
Composition example:
f(x) = x + 1, g(x) = 2x
Step 1: g(f(x)) = 2(x + 1)
Step 2: Simplify → 2x + 2
Inverse example:
f(x) = 5x − 7
Step 1: y = 5x − 7
Step 2: x = 5y − 7
Step 3: y = (x + 7) / 5
f⁻¹(x) = (x + 7) / 5
Tips to Understand Functions
Identify domain and range
Check if function is one-to-one (unique mapping) or onto (covers all values)
Graphs:
Linear → straight line
Quadratic → parabola
Cubic → S-shaped
Trigonometric → periodic curves
Inverse exists only for one-to-one functions
Visit this link for further practice!!
https://besidedegree.com/exam/s/academic