1.5.0 Review of Linear, Quadratic, and Cubic Equations
1.5.1 Linear Equations
Definition:
An equation of degree 1 (highest power of variable = 1).
General form: ax + b = 0, a ≠ 0
Characteristics:
Graph: Straight line
Root: x = -b/a
Can have one variable (x) or two variables (x, y)
Example: 3x + 7 = 0
3x + 7 = 0 or 3x = -7 or x = -7/3
Example: 2x + 5y = 10, y = 2
2x + 5(2) = 10 or 2x + 10 = 10 or 2x = 0 or x = 0
Tips:
Linear equations have only one straight line graph
No curve, vertex, or turning point

1.5.2 Quadratic Equations
Definition:
Equation of degree 2 (highest power of variable = 2)
General form: ax² + bx + c = 0, a ≠ 0
Characteristics:
Graph: Parabola
Vertex: Turning point, x-coordinate = -b/(2a)
Line of symmetry: x = -b/(2a)
Discriminant: Δ = b² - 4ac
Δ > 0 → two real & distinct roots
Δ = 0 → two real & equal roots
Δ < 0 → two complex roots
Methods to Solve Quadratics:
Factorization: ax² + bx + c = 0 or (x - p)(x - q) = 0 or x = p or x = q
Quadratic formula: x = [-b ± √(b² - 4ac)]/(2a)
Completing the square: ax² + bx + c = a(x + b/2a)² + (4ac - b²)/4a
Example: x² - 5x + 6 = 0
x² - 5x + 6 = 0 or (x - 2)(x - 3) = 0 or x = 2 or x = 3
Graphical Understanding:
Parabola opens upwards if a > 0
Parabola opens downwards if a < 0
Vertex gives maximum or minimum value of y
Example (Vertex): y = 2x² - 8x + 5
Vertex x-coordinate = -b/(2a) = 8/(4) = 2
Vertex y-coordinate = y = 2(2)² - 8(2) + 5 = -3
Vertex = (2, -3)
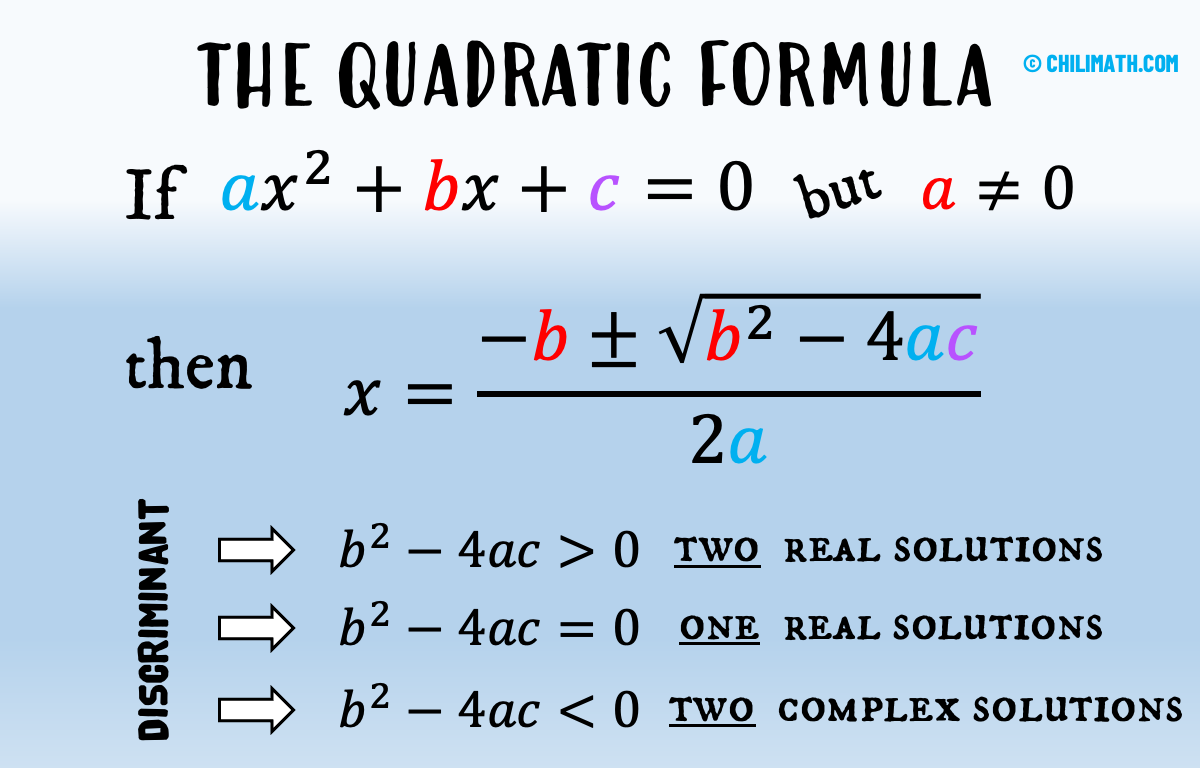
1.5.3 Cubic Equations
Definition:
Equation of degree 3 (highest power of variable = 3)
General form: ax³ + bx² + cx + d = 0
Characteristics:
Graph: Curve passing through origin (simplest case y = x³)
Can have 1 or 3 real roots
May change concavity (point of inflection)
Factoring Method:
Factor by grouping
Trial roots (x = 1, 2, 3, -1, -2, etc.)
Synthetic division
Example: x³ - 6x² + 11x - 6 = 0
x³ - 6x² + 11x - 6 = 0 or (x - 1)(x - 2)(x - 3) = 0 or x = 1 or x = 2 or x = 3
Tips:
Maximum of three real roots
If cubic has complex roots, they occur in conjugate pairs
1.5.4 General Theoretical Knowledge
1. Roots of Equations:
Linear: one root
Quadratic: two roots (may be equal or complex)
Cubic: three roots (may be repeated or complex)
2. Nature of Roots Using Discriminant (Quadratic):
Δ = b² - 4ac
Δ > 0 → two real & distinct roots
Δ = 0 → two real & equal roots
Δ < 0 → two complex roots
3. Graphical Interpretation:
Linear → straight line
Quadratic → parabola (vertex gives max/min)
Cubic → S-shaped curve (point of inflection)
4. Vertex of Quadratic Function:
x-coordinate = -b/(2a) or y = f(-b/(2a))
Maximum value if a < 0, minimum value if a > 0
5. Symmetry:
Quadratic: Symmetric about vertical line x = -b/(2a)
Cubic: No symmetry unless simplified to x³
6. Factorization Tips:
Always check for common factors first
Use grouping for cubic equations
Quadratic: Look for two numbers multiplying to ac and adding to b
1.5.5 Additional Examples
Example 21: Solve 3x² - x - 10 = 0
3x² - x - 10 = 0 or (3x + 5)(x - 2) = 0 or x = -5/3 or x = 2
Example 22: Solve x³ + 4x² - x - 4 = 0
x³ + 4x² - x - 4 = 0 or (x³ + 4x²) - (x + 4) = 0 or x²(x + 4) - 1(x + 4) = 0 or (x² - 1)(x + 4) = 0 or (x - 1)(x + 1)(x + 4) = 0 or x = 1 or x = -1 or x = -4
Example 23: Solve 2x³ - 3x² - 8x + 12 = 0
2x³ - 3x² - 8x + 12 = 0 or (2x³ - 3x²) - (8x - 12) = 0 or x²(2x - 3) - 4(2x - 3) = 0 or (2x - 3)(x² - 4) = 0 or (2x - 3)(x - 2)(x + 2) = 0 or x = 3/2 or x = 2 or x = -2
Example 24: Solve y = x² + 6x + 5 graphically
y = x² + 6x + 5 = 0 or (x + 1)(x + 5) = 0 or x = -1 or x = -5
Example 25: Solve y = x³ - x
y = x³ - x = 0 or x(x² - 1) = 0 or x(x - 1)(x + 1) = 0 or x = 0 or x = 1 or x = -1