5.0 Review: Area and Perimeter/Circumference of Basic Plane Shapes
Name of ShapeAreaPerimeter/CircumferenceSquareA = l² square unitsP = 4l unitsRectangleA = l × b square unitsP = 2(l + b) unitsParallelogramA = base × height square unitsP = 2(sum of adjacent sides) unitsTriangleA = (1/2) × base × height square unitsP = sum of all three sides unitsEquilateral TriangleA = (√3/4) × side² square unitsP = 3 × side unitsRhombusA = (1/2) × diagonal1 × diagonal2 square unitsP = 4 × side unitsTrapeziumA = (1/2) × (sum of parallel sides) × height square unitsP = sum of all four sides unitsQuadrilateral (general)No single formula (depends on type)P = sum of all four sides unitsCircleA = πr² square units or A = πd²/4 square unitsC = 2πr = πd units
Note: For herb (dubo) planted in rectangular field minus circular cricket ground: Area for herb = Area of rectangle – Area of circle = l × b – πr²

5.1 Area of Pathways
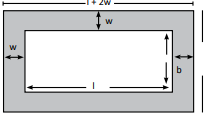
A. Outer Path Around Rectangle
- Outer dimensions: length = l + 2w, breadth = b + 2w
- Area of path = (l + 2w)(b + 2w) – l × b = 2w(l + b + 2w) square units
Special case (Square): l = b → Area = 4w(l + w) square units
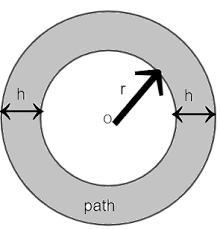
Outer Circular Path Around Circle
- Area of path = π(r + w)² – πr² = πw(2r + w) square units
- If diameter d given: πw(d + w) square units
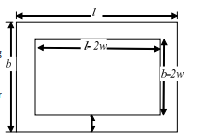
B. Inner Path Around Rectangle
- Inner dimensions: length = l – 2w, breadth = b – 2w
- Area of path = l × b – (l – 2w)(b – 2w) = 2w(l + b – 2w) square units
Special case (Square): 4w(l – w) square units
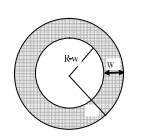
Inner Circular Path Around Circle
- Area of path = πR² – π(R – w)² = πw(2R – w) square units
- If diameter d given: πw(d – w) square units
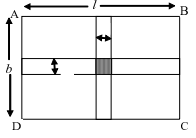
C. Cross Paths (Perpendicular at Middle)
- Two paths cross, forming a + shape
- Area = (l × w) + (b × w) – w² (subtract overlapping square)
- = w(l + b – w) square units
D. Cost of Paving Paths
- Number of tiles/stones N = (Area of path) / (Area of one tile)
- Total cost = N × cost per tile
5.2 Surfaces of Room
5.2.1 Area of Four Walls, Floor, and Ceiling
- Area of four walls = 2h(l + b) square units
- Area of floor + ceiling = 2(l × b) square units
- Total (four walls + floor + ceiling) = 2(lh + bh + lb) square units
Excluding doors/windows: Paintable/plaster area = Area of four walls – (total area of doors + windows)
5.2.2 Cost of Carpeting, Painting, Plastering, etc.
- Total cost = Area × rate per square unit
Important Solved Examples (Selected)
Q1. Find area and perimeter of a square of side 14 m.
Area = side × side
Area = 14 × 14
Area = 196 m²
Perimeter = 4 × side
Perimeter = 4 × 14
Perimeter = 56 m
Q2. Find area of a rectangle 20 m × 14 m.
Area = length × breadth
Area = 20 × 14
Area = 280 m²
Q3. A circular path of width 3 m surrounds a circle of radius 14 m. Find area of path.
Formula: Area of path = πw(2r + w)
= (22/7) × 3 × (2 × 14 + 3)
= (22/7) × 3 × 31
= 290.14 m²
Q4. Find area of four walls of a room 10 m × 8 m × 5 m.
Formula: Area of four walls = 2h(l + b)
= 2 × 5 × (10 + 8)
= 10 × 18
= 180 m²
Q5. Cost of painting walls at Rs. 15 per m² if area = 180 m².
Cost = Area × Rate
Cost = 180 × 15
Cost = Rs. 2700
Q6. Find area of inner path of width 2 m inside a square of side 20 m.
Formula: Area of inner path = 4w(l − w)
= 4 × 2 × (20 − 2)
= 8 × 18
= 144 m²
Q7. Find area of two cross paths of width 4 m in a rectangle 60 m × 40 m.
Formula: Area of cross paths = w(l + b − w)
= 4 × (60 + 40 − 4)
= 4 × 96
= 384 m²
Q8. Find area of a circle of radius 7 m.
Area = πr²
= (22/7) × 7 × 7
= 154 m²
Q9. Find number of tiles of area 0.25 m² needed to cover 100 m².
Number of tiles = Total area ÷ Area of one tile
= 100 ÷ 0.25
= 400 tiles
Q10. Find cost of carpeting a floor 8 m × 6 m at Rs. 120 per m².
Area = 8 × 6 = 48 m²
Cost = 48 × 120
Cost = Rs. 5760
Q11. Find height of room if area of four walls is 360 m², length = 15 m, breadth = 9 m.
Area of four walls = 2h(l + b)
360 = 2h(15 + 9)
360 = 48h
h = 7.5 m
Q12. Find area of a trapezium with parallel sides 12 m and 20 m, and height 10 m.
Area = ½ × (sum of parallel sides) × height
= ½ × (12 + 20) × 10
= ½ × 32 × 10
= 160 m²
For further practice visit this link !!
https://besidedegree.com/exam/s/academic