Ratio and Proportion

A ratio is a comparison of two quantities of the same kind.

Example: White button mushrooms cost Rs. 300 per kg, oyster mushrooms Rs. 150 per kg. Ratio = 300:150 = 2:1.

Ratio tells how many times one quantity is of another.

Proportion

Proportion is an equation stating that two ratios are equal.

Example: 2:4 = 4:8 since 2/4 = 4/8 = 1/2.

If two or more ratios are equal, they are in proportion.

Properties of Proportion

Invertendo: If a:b = c:d, then b:a = d:c

Alternendo: If a:b = c:d, then a:c = b:d

Componendo: If a:b = c:d, then (a+b):b = (c+d):d

Dividendo: If a:b = c:d, then (a-b):b = (c-d):d

Componendo and Dividendo: If a:b = c:d, then (a+b):(a-b) = (c+d):(c-d)

Addendo: If a:b = c:d, then (a+c):(b+d) = a:b = c:d

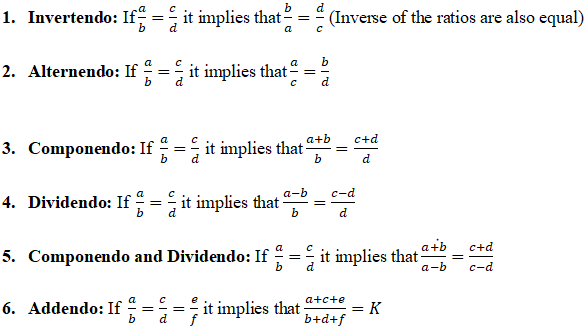
Examples for Properties

Example 1:
If 4:3 = b:a, find (4a+2b):(4a+3b).
Solution:
Or, 4:3 = b:a ⇒ 4a = 3b
Or, (4a+2b):(4a+3b) = (3b+2b):(3b+3b)
Or, = 5b:6b = 5:6

Example 2:
If b:a = 6:5, find (6a-2b):(5a+2b).
Solution:
Or, b/a = 6/5 ⇒ a/b = 5/6
Or, (6a-2b)/(5a+2b) = (6×5/6 - 2)/(5×5/6 + 2)
Or, = (5-2)/(25/6 + 2) = 3/(25/6 + 12/6)
Or, = 3/(37/6) = 18/37
Or, Answer = 18:37

Example 3:
If (4a-5b):(5a+4b) = 1:3, find a:b.
Solution:
Or, (4a-5b)/(5a+4b) = 1/3
Or, 3(4a-5b) = 5a+4b
Or, 12a-15b = 5a+4b
Or, 12a-5a = 4b+15b ⇒ 7a = 19b
Or, a:b = 19:7

Example 4:
If ratio of two numbers is 5:6, sum = 33, find numbers.
Solution:
Or, Let numbers x and y ⇒ x:y = 5:6 ⇒ 6x = 5y
Or, x+y = 33 ⇒ y = 33-x
Or, 6x = 5(33-x) ⇒ 6x = 165-5x
Or, 6x+5x = 165 ⇒ 11x = 165 ⇒ x = 15
Or, y = 33-15 = 18
Or, Numbers = 15,18

Example 5:
Divide 455 in ratio 6:7.
Solution:
Or, Let parts 6k,7k ⇒ 6k+7k=455 ⇒ 13k=455 ⇒ k=35
Or, 6k=210, 7k=245
Or, Answer = 210,245

Continued Proportion

Numbers a,b,c,d... are in continued proportion if a:b = b:c = c:d = ...

Example: 2:4:8:16

Example:
If a:b = b:c = c:d, prove (a-b)/(c-d) = (a+b)/(c+d)
Solution:
Or, Let a:b = b:c = c:d = k ⇒ a=bk, c=dk
Or, LHS = (a-b)/(c-d) = (bk-b)/(dk-d) = k(b-1)/(d-1) = RHS

Important Solved Questions

1.Divide Rs. 810 in the ratio 7 : 8
Or, Let parts = 7k, 8k ⇒ 7k + 8k = 810 ⇒ 15k = 810 ⇒ k = 54
Or, 7k = 378, 8k = 432

2.Two numbers are in the ratio 3 : 2 and difference = 5
Or, Let numbers = 3x, 2x ⇒ 3x – 2x = 5 ⇒ x = 5
Or, Numbers = 15 and 10

3.Two numbers in ratio 7 : 9, sum = 80
Or, 7x + 9x = 80 ⇒ 16x = 80 ⇒ x = 5
Or, Numbers = 35 and 45

4.Two numbers in ratio 8 : 5. If 6 added, ratio = 3 : 2
Or, (8x + 6)/(5x + 6) = 3/2
Or, 2(8x + 6) = 3(5x + 6) ⇒ 16x + 12 = 15x + 18
Or, x = 6 ⇒ Numbers = 48, 30

5.Father and son ages in ratio 5 : 3, difference = 30
Or, 5x – 3x = 30 ⇒ 2x = 30 ⇒ x = 15
Or, Ages = 75, 45

6.Mother and daughter ratio 3 : 1, after 5 years ratio = 5 : 2
Or, Let ages = 3x, x ⇒ (3x + 5)/(x + 5) = 5/2
Or, 2(3x + 5) = 5(x + 5) ⇒ 6x + 10 = 5x + 25
Or, x = 15 ⇒ Ages = 45, 15

7.Present market price of mushrooms
Or, Let oyster = x, white button = 3x
Or, After Rs. 50 rise: (x + 50)/(3x + 50) = 3/7
Or, 7(x + 50) = 3(3x + 50) ⇒ 7x + 350 = 9x + 150 ⇒ 2x = 200 ⇒ x = 100
Or, Oyster = 100, White button = 300

8.Divide 192 oranges in 7 : 9 ratio
Or, 7x + 9x = 192 ⇒ 16x = 192 ⇒ x = 12
Or, 7x = 84, 9x = 108

9.Numbers in ratio 4 : 5, difference = 20
Or, 5x – 4x = 20 ⇒ x = 20 ⇒ Numbers = 80, 100

10.Numbers in ratio 6 : 5, sum = 66
Or, 6x + 5x = 66 ⇒ 11x = 66 ⇒ x = 6
Or, Numbers = 36, 30

For further practice visit this link !!

https://besidedegree.com/exam/s/academic