2.0 REVIEW : LIMIT OF A FUNCTION
Idea (Polygon to Circle Analogy):
As the number of sides of a polygon increases more and more, the shape becomes closer to a circle.
Hence, when number of sides becomes very large, polygon behaves like a circle.
Meaning of Limit:
The limit of a function at a point is the value that the function approaches when x comes very close to that point from both sides.
Example 1 : Limit of f(x) = x square at x = 2
We observe values of x close to 2 from left and right.
Left side values (x less than 2):
x = 1.9
then y = 1.9 × 1.9 = 3.61
x = 1.99
then y = 1.99 × 1.99 = 3.9601
x = 1.999
then y = 1.999 × 1.999 = 3.996001
Values are getting closer to 4.
Right side values (x greater than 2):
x = 2.0001
then y = 2.0001 × 2.0001 = 4.00040001
x = 2.001
then y = 2.001 × 2.001 = 4.004001
x = 2.01
then y = 2.01 × 2.01 = 4.0401
Values are again getting closer to 4.
Conclusion:
Left-hand value = 4
Right-hand value = 4
Since both are equal, the limit exists and is equal to 4.
Condition for Existence of Limit:
Limit exists at x = a if
left-hand value = right-hand value.
Formal Idea of Limit:
If values of f(x) become very close to a fixed number L when x is very close to a number a, then the limit of f(x) at a is L.
Example 2 : Limit of f(x) = (x square minus 1) divided by (x minus 1) at x = 1
At x = 1, the function is not defined.
Now check values near 1.
x = 0.99
then f(x) = (0.99 square minus 1) divided by (0.99 minus 1)
then f(x) is approximately 2
x = 1.01
then f(x) is approximately 2
Both sides approach 2.
Conclusion:
Limit exists and is equal to 2, but function is not defined at x = 1.
This is a removable discontinuity.
Example 3 : Limit of f(x) = 3x + 1 at x = 2
Substitute x = 2.
f(2) = 3 × 2 + 1 = 7
Left-hand and right-hand values are both 7.
Conclusion:
Limit exists and equals function value.
Function is continuous at x = 2.
2.1 CONTINUITY IN DIFFERENT SETS OF NUMBERS
Natural Numbers:
There are gaps between numbers.
Example: no natural number between 4 and 5.
Hence discontinuous.
Integers:
Also have gaps.
Hence discontinuous.
Rational Numbers:
Between any two rationals, irrational numbers exist.
Hence not continuous.
Real Numbers:
No gaps on number line.
Between any two real numbers, infinite real numbers exist.
Hence continuous.
Real-Life Examples of Continuity:
Flow of river water
Change in temperature
Growth of plant height
Real-Life Examples of Discontinuity:
Attendance of students in class
Jumping of frog
Number of cars passing signal per minute
2.2 CONTINUITY AND DISCONTINUITY IN GRAPHS
Continuous Graph:
Graph drawn without lifting pen.
No break, gap, jump, or hole.
Discontinuous Graph:
Graph has break, jump, gap, or hole.
Example 4 : Straight line y = x + 2
Graph is smooth and unbroken everywhere.
Hence continuous for all x.
Example 5 : Step Function
Graph has jumps at certain x-values.
Hence discontinuous at jump points.
Continuous only within each interval.
2.3 SYMBOLIC REPRESENTATION OF CONTINUITY
A function is continuous at x = a if:
Function is defined at x = a
Left-hand value equals right-hand value
That value equals f(a)
Example 6 : f(x) = (x square minus 9) divided by (x minus 3)
At x = 3, function is not defined.
Simplify expression:
x square minus 9 = (x minus 3)(x plus 3)
After simplification, f(x) = x + 3 for x not equal to 3.
Now check values near 3.
x = 2.99
then f(x) approximately equals 5.99
x = 3.01
then f(x) approximately equals 6.01
Both sides approach 6.
Conclusion:
Limit exists and equals 6, but function is not defined at x = 3.
Hence removable discontinuity.
Example 7 : Quadratic Function f(x) = x square + 4x + 1
Quadratic functions have no breaks or gaps.
Hence continuous for all real values of x.
Example 8 : Piecewise Function
f(x) = x + 1 for x less than 2
f(x) = 3x minus 1 for x greater than or equal to 2
Check at x = 2.
Left value = 2 + 1 = 3
Right value = 3 × 2 minus 1 = 5
Since values are not equal, function is discontinuous at x = 2.
So function is discontinuous at x = 1.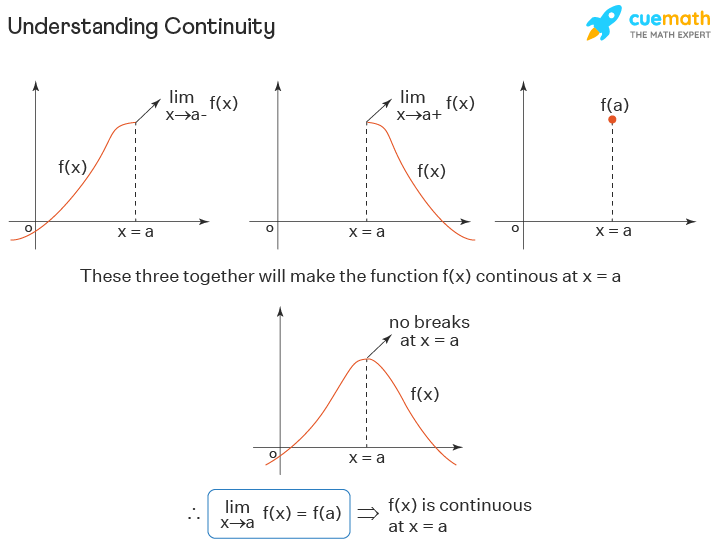
IMPORTANT PRACTICE QUESTIONS
Find limit of f(x) = 2x + 5 at x = 3
Check continuity of f(x) = x square at x = 1
Find limit of (x square minus 4) divided by (x minus 2) at x = 2
Give two real-life examples of continuity and discontinuity
Check continuity of a given piecewise function at a point
Visit this link for further practice!!
https://besidedegree.com/exam/s/academic
